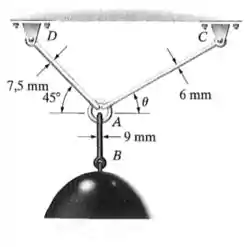
A luminária de é sustentada por três hastes de aço interligadas por um anel em . Determine o ângulo de orientação de de modo que a tensão normal média na haste seja duas vezes a tensão normal média na haste .
Qual é a intensidade da tensão em cada haste? O diâmetro de cada haste é dado na figura.
Passo 1
Galera, para começar esse problema que tal fazermos um diagrama de corpo livre? O ponto está sobre ação de três forças de tração:
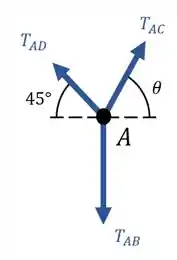
O valor de uma dessas forças foi dado pelo exercício: a haste deve exercer uma força de tração suficiente para sustentar a luminária de no ponto . Isso significa que:
A partir daí vamos analisar quais serão as tensões internas e também vamos utilizar um pouquinho de trigonometria para resolver este problema, beleza?
Lembre-se que o exercício quer saber qual o ângulo para que . O exercício também quer saber os valores de , e nesse caso.
Passo 2
Que tal lembramos agora então a definição da tensão normal? É basicamente a força normal sobre a área:
Gente, nesse caso as trações são as próprias forças normais ok? Porque atuam no sentido axial. E são todas trativas porque esticam as hastes. Então vamos ter o seguinte:
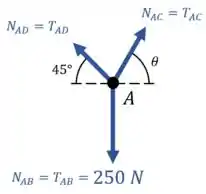
Show de bola!
Mais e aí? Como vamos encontrar ?
- Vamos ter que fazer o equilíbrio de forças no ponto . Isso vai gerar um sistema de equações.
- Desse sistema de equações vamos encontrar , em função de ;
- Com isso e com as áreas e já calculadas, vamos encontrar e também em função de ;
- Finalmente, vamos usar a relação para encontrar o valor de !
Passo 3
Agora é hora do equilíbrio de forças no ponto :
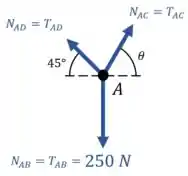
Com ajuda da imagem acima, conseguimos fazer o equilíbrio de forças na vertical e na horizontal.
Só precisamos tomar o cuidado de decompor devidamente as forças e em suas componentes em e em !
Para a vertical, o equilíbrio de forças fica assim:
Calculando as componentes e substituindo :
Vamos guardar essa equação para o nosso futuro sistema de equações!
E agora, o equilíbrio de forças para a horizontal:
Calculando as componentes:
Com isso, nosso sistema de equações fica pronto:
Substituindo os valores de e nós vamos ter:
Reorganizando:
Passo 4
Pessoal, até dá para resolver esse sistema “na marra” mas vamos fazer de uma forma mais esperta. Para isso vamos trazer a seguinte relação:
Agora temos de calcular as áreas. As áreas , e podem ser calculadas a partir dos diâmetros , e .
Começando pelo cálculo das áreas das seções transversais usando a fórmula da área circular :
Substituindo o valor dos diâmetros:
Então se a gente substituir essas áreas na relação de tensões vamos ter:
Agora olha só o nosso sistema:
Substituindo a relação entre e encontrada na segunda equação vamos ter:
Logo,
Então já achamos a primeira parte do problema que é achar o ângulo . Agora temos de encontrar as tensões.
Passo 5
Com o ângulo encontrado, agora só falta calcular as tensões em cada haste. Para isso vamos precisar das tensões e . Para isso vamos substituir no nosso sistema:
Nós já sabemos que
Então vamos substituir na primeira equação junto com o valor do :
E o valor de será dado por:
Passo 6
Agora é só utilizar a equação da tensão normal média. Usando a fórmula da tensão normal média para a tensão na haste , :
Substituindo os valores e :
Para vamos ter:
Nós já temos a área e a força :
Substituindo:
E para :
A área e força são dadas por:
Substituindo: