O mancal de encosto está sujeito às cargas mostradas. Determine a tensão normal média desenvolvida nas seções transversais que passam pelos pontos , e .
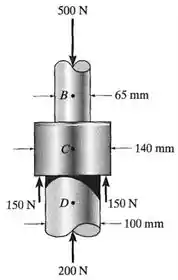
Passo 1
Para calcular as tensões normais médias , precisamos encontrar o módulo das forças normais internas e o valor das áreas de cada seção transversal.
As áreas podem ser encontradas a partir dos diâmetros fornecidos , e .
Para encontrar as forças internas, vamos precisar nos lembrar da matéria de esforços internos: vamos ter que realizar seções em , e , fazer o diagrama de corpo livre (“DCL”) dessas seções e avaliar as condições de equilíbrio.
Passo 2
Vamos começar calculando as áreas de cada seção!
As 3 seções transversais são circulares e nos foi fornecido os seus diâmetros , então podemos usar a fórmula de área do círculo .
Para a seção , temos:
Para a seção :
E finalmente para :
Passo 3
Agora vamos ter que calcular as forças internas em cada uma das 3 seções: , e .
Nesse exercício, só importa para a gente a intensidade da força interna (não precisamos nos preocupar com a direção ou sinal dessa força.)
Isso significa que podemos fazer uma análise um pouco mais “nas coxas”:
- Para cada seção, escolhemos entre fazer o DCL da parte da peça superior à seção (como foi feito com as seções e na imagem abaixo) ou fazer o DCL da parte inferior à seção (como feito para a seção ).
- Em cada DCL, desenhamos as forças externas (em azul na imagem) atuantes nessa parte da peça. Depois desenhamos forças internas (em vermelho) de forma a balancear as forças externas e destacamos os valores encontrados para elas.
Na prática, essa análise fica assim:
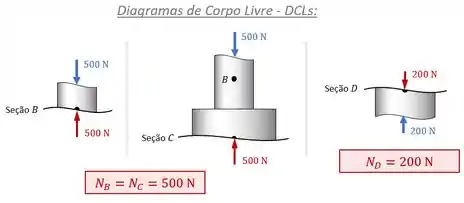
Passo 4
Agora temos tudo em mãos para calcular as tensões com a fórmula .
Para a seção , e :
Para , e :
E finalmente, para , e :