Sabendo que a porção central da barra tem uma área de seção transversal uniforme de , determine a intensidade da carga para qual a tensão normal naquela parte de é .
Passo 1
Inicialmente, vamos ignorar o desenho e começar prestando atenção no enunciado do exercício.
A barra possui uma tensão normal média e uma área de seção transversal .
Com essas informações, nós podemos aplicar a equação da tensão normal média () na barra para encontrar a força normal interna :
Só tem um problema, o exercício não quer saber o valor da força na situação em que , ele quer saber o valor da força nessa situação.
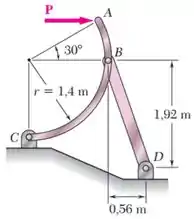
Então vamos observar o desenho: como é que a força se relaciona com o que está ocorrendo na barra ?
A barra está apoiando a barra curva , contribuindo de alguma forma para o seu equilíbrio.
Esse apoio se dá através de uma força de apoio que pode estar na direção da barra ou em outra direção, como mostra a imagem:
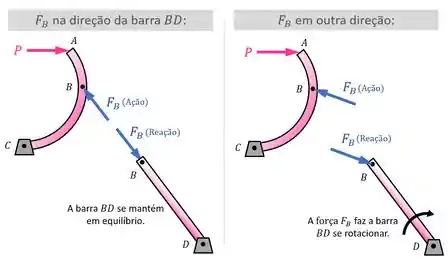
Como a barra deve se manter em equilíbrio, concluímos que está na direção da barra.
Por outro lado, como a barra curva deve se manter em equilíbrio, a força deve gerar, em relação ao ponto , um momento contrário ao momento gerado pela força .
Esse equilíbrio de momentos vai relacionar e .
Mas espera aí, a força , desse jeito, na direção da barra , realizando compressão, gera uma força interna normal de mesma intensidade:
Então o equilíbrio de momentos vai nos permitir relacionar e .
E nós já vamos ter descoberto usando a equação da tensão normal média e assim vamos resolver o exercício!
Passo 2
Vamos começar calculando a força interna a partir da equação da tensão normal média:
Como e :
Lembrando que , chegamos ao resultado:
Passo 3
O próximo passo é relacionar e através do equilíbrio de momentos da barra curva .
Para fazer isso, vamos desenhar o Diagrama de Corpo Livre de :
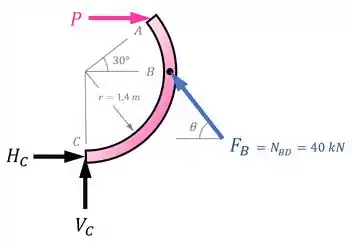
Para fazer o equilíbrio de momentos em relação ao ponto , vamos querer decompor a força em suas componentes vertical e horizontal, para que os seus braços sejam fáceis de calcular.
Para facilitar o cálculo do braço da força , já vamos também deixar calculado a distância entre as linhas horizontais que passam pelos pontos e .
Com essas duas mudanças, o diagrama de corpo livre de fica assim:
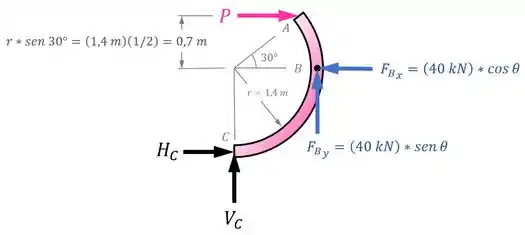
Realizando o equilíbrio de momentos em relação ao ponto :
Substituindo e :
A única coisa que nos falta agora é encontrar os valores de e .
Passo 4
O ângulo é o ângulo que a força faz em relação à horizontal, e, consequentemente, é o ângulo que a barra faz em relação a horizontal:
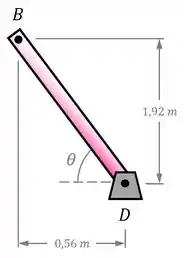
Dessa imagem, podemos calcular o valor de seno e cosseno de em função do comprimento da barra:
O valor de pode ser encontrado pelo teorema de Pitágoras:
Com isso, encontramos e :
Passo 5
Voltando para a equação que tínhamos encontrado anteriormente:
Substituindo os valores de e :