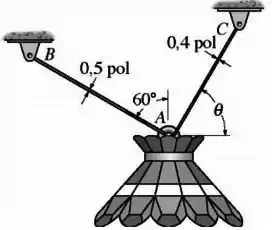
A luminária de é suportada por duas hastes de aço acopladas por um anel em . Determinar qual das hastes está sujeita à maior tensão normal média e calcular seu valor. Sabemos que . O diâmetro de cada haste é dado na figura.
Passo 1
Para descobrir qual haste está sujeita à maior tensão normal média, vamos precisar calcular a tensão em cada haste.
Então, para calcular essas tensões , vamos precisar da força interna em cada haste e da área da seção transversal de cada haste.
As hastes estão sendo tracionadas para suportar o peso da luminária . Se fizermos um equilíbrio de forças no ponto , vamos descobrir o valor das forças de tração nas hastes:
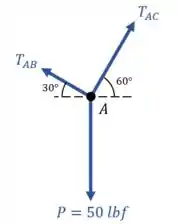
Como as hastes só sofrem essas forças de tração, podemos garantir que as forças internas serão iguais a essas forças de tração. Daí encontramos que e .
Já para encontrar as áreas e , vamos ter que usar os diâmetros fornecidos: e .
Passo 2
Para encontrar as forças de tração e consequentemente as forças internas , vamos voltar para o diagrama de forças no ponto :
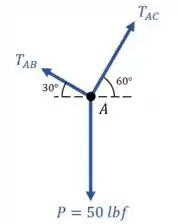
Lembra aí, o equilíbrio de forças acontece quando o somatório de forças é igual a zero ().
Um jeito de ver isso é vendo se a soma das forças na vertical dá zero () e se a soma das forças na horizontal dá zero ().
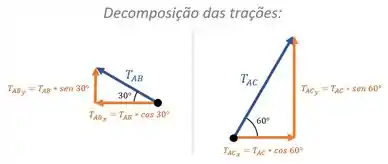
Para fazer essas somas, vamos ter que decompor as trações em suas componentes verticais e horizontais.
Isso significa ter que usar seno e cosseno para encontrar essas componentes, como mostra a imagem abaixo:
Passo 3
Com a decomposição das forças já feita, agora podemos fazer os equilíbrios de forças na vertical e na horizontal!
Equilíbrio de forças na vertical:
Como na vertical temos as componentes verticais de e apontando para cima e a força peso apontando para baixo, essa expressão acima fica assim:
Como encontramos na decomposição das trações que e :
Vamos guardar essa equação por enquanto!
Em seguida vem o equilíbrio de forças na horizontal:
Como na horizontal temos a componente horizontal de apontando para a direita e a componente horizontal de apontando para a esquerda:
Substituindo os valores e encontrados na decomposição de forças
Vamos também guardar essa equação!
Passo 4
As duas equações que guardamos no passo anterior compõem um sistema de equações:
Se resolvermos esse sistema, encontraremos e (e consequentemente e !)
Bora resolver!
Da segunda equação, encontramos que:
Substituindo esse valor de na primeira equação:
Como :
Substituindo esse valor na segunda equação do sistema:
Pronto! Agora podemos dizer que encontramos e !
Passo 5
Calculando as áreas das seções transversais das hastes com a fórmula :
Como :
E como :
Passo 6
Temos as forças internas e as áreas ! Hora de calcular as tensões:
Substituindo os valores encontrados nos últimos dois passos:
Passo 7
Calculadas as tensões, vemos como a maior tensão é , mas, antes de anunciar o resultado do problema, temos mais uma coisa para observar!
Existe uma unidade utilizada para pressão e tensão chamada . O nome dessa unidade vem do inglês pounds(-force) per square inch.
Traduzindo para o português, fica libras-força por polegadas ao quadrado, que é exatamente o que temos no nosso resultado.
Isso significa que podemos reescrever nosso resultado assim: