Calcule o com uma expansão em cofatores ao longo de uma linha ou coluna de sua escolha.
Passo 1
Bom galerinha, podemos escolher qual linha ou coluna usar, então optamos pela menos trabalhosa !!
Que tal a coluna?
Vamos dar uma olhada como ficaria este determinante?
Agora vamos substituir?
Então, precisamos achar os cofatores , e , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula meio chatinha, mas vamos fazer devagar:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Agora precisamos lembrar de duas regrinha muito importante
- Número negativo elevado a expoente par fica positivo
- Número negativo elevado a expoente ímpar continua negativo
Então nossos cofatores ficarão
Passo 2
Para achar aqueles alí, que são chamados de menor complementar, vamos excluir a linha e a coluna do elemento, ok?
Para o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:
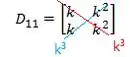
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E assim achamos um dos cofatores !!
Passo 3
Para achar nós cortamos a linha e a coluna
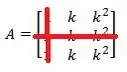
E com o que sobrou vamos montar um novo determinante (aqui eu já multipliquei todo mundo por pois vamos precisar desse valor negativo para calcular o ):
Já vimos que o determinante dessa mesma matriz ali em cima!
Então:
Passo 4
Para o elemento é nós cortamos a linha e a coluna
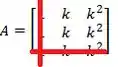
E com o que sobrou vamos montar um novo determinante:
Então:
E agora vamos colocar no determinante?
E assim a gente fecha mais uma!!