Considerando a matriz
Ache o menor complementar do elemento
Passo 1
Para este exercício, vamos precisar ter bem fresco na cabeça o conceito de menor complementar !!
O menor complementar pode ser representado por , onde representa a linha em que ele se encontra e a sua coluna
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Quer saber de uma coisa? O determinante dessa matriz aí de cima é o que a gente chama de menor complementar! Vamos calcular ele. Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:
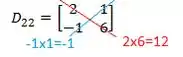
E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
E assim achamos o menor complementar !!