Encontre o determinante da matriz expandindo em cofatores ao longo da primeira linha:
Passo 1
Bora dificultar esse negócio? Hahahah ...
Brincadeira galerinha, vamos é facilitar!!
Para calcular um determinante usando o Teorema de Laplace vamos escolher uma linha ou coluna qualquer, de preferência a que tenha mais zeros, e usar a seguinte relação:
Usei aqui os elemento da primeira linha, porque o problema pediu isso, certo?
Agora vamos substituir?
Então, só precisamos achar os cofatores e , ok?
Já sabemos que o cofator do elemento é calculado usando essa formulinha aqui:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
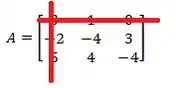
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então:
E assim achamos um dos cofatores !!
Passo 3
Para o elemento nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso multiplicamos os números presentes sobre a diagonal vermelha e azul:

E o determinante é o valor da direita (vermelho) menos o da esquerda (azul):
Então, como :
E agora vamos colocar no determinante?
Legal, não foi ?!