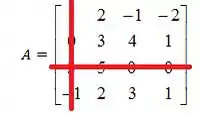
Seja
Encontre o determinante da matriz expandindo em cofatores.
Passo 1
Já sabemos como calcular os determinantes, certo?
Então o primeiro passo será escolher qual linha ou coluna vamos utilizar !! Vamos escolher aquela que possui mais zeros, para facilitar nossa vida, ok?
Vamos optar pela terceira linha? É um bom plano... tem dois zeros ali, acho que serve!
Vamos dar uma olhada como ficaria este determinante?

Agora vamos substituir?
Então, precisamos achar os cofatores e , ok?
Já sabemos que o cofator do elemento é calculado usando uma fórmula bem tranquilinha:
Onde representa a linha em que ele se encontra e a sua coluna !!
Para o caso que estamos analisando:
Passo 2
Para achar o menor complementar vamos excluir a linha e a coluna do elemento, ok?
Como o elemento é nós cortamos a linha e a coluna
E com o que sobrou vamos montar um novo determinante:
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:
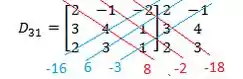
E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Passo 3
Como o elemento é nós cortamos a linha e a coluna

E com o que sobrou vamos montar um novo determinante (aqui eu já multipliquei tudo por menos pois vai ajudar a gente mais para frente):
E agora sim vamos resolver este determinante que já é bem mais simples! Para isso vamos adicionar ao lado dessa matriz a primeira e a segunda coluna:
Agora multiplicamos os números presentes sobre a diagonal vermelha e azul:

E para achar o determinante somamos os valores da direita (vermelho) e substraímos pela soma dos elementos da esquerda (azul):
Então, como :
Achando o determinante:
E assim achamos o determinante !!