Determine a transformada de Laplace da função
Passo 1
Opaa, vamos lá! A questão quer que a gente calcule a transformada de Laplace da função:
Pra começar, vamos lembrar que se:
Aí você me pergunta: “Amigo, como eu resolvo se eu não lembrar dessa relação trigonométrica?” Eu te digo, não faz. Tem que lembrar. E como faz pra lembrar? Fazendo muito exercício! Quanto mais exercício você faz, esses detalhes vemesses detalhes vêm automaticamente. Confia em mim
Então:
Daí a gente pode aplicar a distributiva com e ficar com a função reescrita:
E a transformada vai ser:
Passo 2
Agora, vamos olhar na tabela de transformadas de Laplace qual função mais se parece com o as que a gente quer.
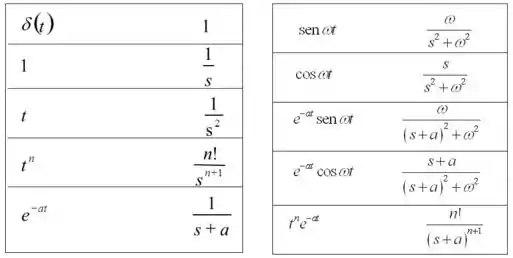
Bem, pra primeira transformada, pela tableatabela, como temos , vamos ficar com:
E pro outro carinha, primeiramente, como estamos multiplicando por uma exponencial, sabemos que vamos começar ignorando o exponencial, certo? E fazemosndo a transformada só do outro termo.
Por tabela, sabemos que a transformada do
TRANQUILO, né? Agora, vamos substituir o por onde é o termo dentro da exponencial, simples assim!
Então teremos
Como estamos trabalhando com temos e , ficamos entãçao com
Ainda temos que lembrar de multiplicar por já que queremos
Juntando os dois termos, teremos: