Uma caixa de é levantada de uma altura de , a partir do repouso, por uma força aplicada vertical de . Encontre a energia cinética final da caixa.
Considere
Passo 1
Faaaala aí galerinha bonita, vamos pra mais uma questão sobre Teorema trabalho- eneriga? Vamos lá!
Bom, vamos começar relembrando o que é o teorema trabalho-energia cinética.
No caso do nosso exercício temos dois trabalhos sendo realizados aqui: o da força que que o guindaste faz e o da gravidade (força peso ). Vamos calcular os dois.
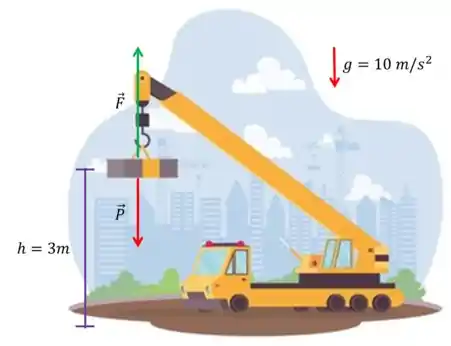
Beleza, vamos separar as informações do enunciado!
Passo 2
Calculando o trabalho realizado pela força aplicada:
Passo 3
Agora vamos calcular o trabalho realizado pela força gravitacional:
Como ele vai da altura até a altura :
Passo 4
Agora vamos aplicar o teorema né?
Como a caixa partiu do repouso, ele não possuía energia cinética nenhuma.
Como a energia cinética inicial da caixa era nula, temos que a energia cinética final é: