Supondo que uma bola de massa se desloque em linha reta puxada por uma linha que aplica força horizontal um percurso de . Sabemos que a bola inicia o trajeto com velocidade de e termina com velocidade igual a . Determine o módulo da força necessária.
Passo 1
Bom pessoal, vamos pensar em todos os dados fornecidos pelo problema! A massa não se altera ao longo do percurso:
A velocidade inicial e final são:
Como temos esses dados, podemos calcular a energia cinética a partir da fórmula:
Passo 2
Vamos calcular a energia cinética inicial, substituindo os valores iniciais:
Que são:
Elevando ao quadrado, temos:
Realizando a multiplicação de por :
Agora basta dividir por , que encontramos a energia cinética igual a:
Passo 3
Quanto a energia cinética final, vamos substituir os valores finais na equação:
Que são:
Elevando ao quadrado, temos:
Realizando a multiplicação de por :
Agora basta dividir por , que encontramos a energia cinética igual a:
Passo 4
Agora para calcular o trabalho, faremos a variação da energia cinética:
A variação da energia cinética, nada mais é do que a energia cinética final menos a energia cinética inicial:
Então podemos dizer que
Vamos substituir os valores das energias que calculamos:
Logo:
Passo 5
Mas você me pergunta: por que eu quero saber do trabalho?
Lembra que o trabalho é o produto da força pelo deslocamento e o ângulo entre eles:
Como ele disse que a força é horizontal e não falou sobre nenhum desnível no percurso, vamos considerar que a força puxa a bola no mesmo sentido do deslocamento:
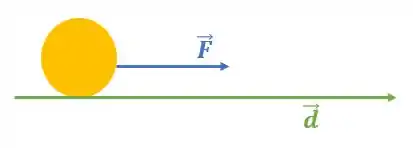
Logo, o ângulo entre os vetores força e deslocamento é
Passo 6
Substituindo os valores dados no enunciado e que encontramos:
Teremos:
Como sabemos o cosseno de é igual a :
Como queremos a força, vamos isolar de um lado da igualdade só:
Que é igual a divisão:
Prontinho, essa era a resposta que queríamos!