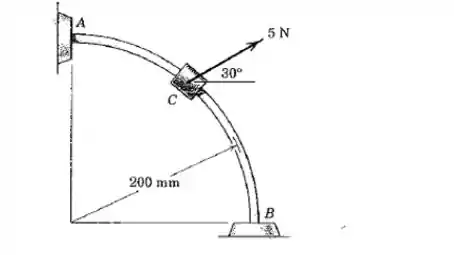
O cursos de parte do repouso em e desliza com atrito desprezível sobre a haste fixa no plano vertical. Determine a velocidade com que o cursor golpeia a extremidade quando atuado por uma força de , que possui uma direção constante. Despreze as pequenas dimensões do cursor.
Passo 1
Podemos representar o sistema pelo desenho abaixo:
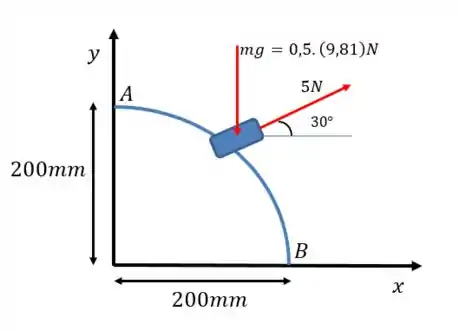
Passo 2
Temos que:
Só que, o trabalho realizado entre será a soma dos trabalhos da força de e do peso.
Passo 3
Vamos analisar primeiro a força de , que é a mais difícil. Veja bem: Existe um componente em , que tem que ser multiplicada pela distância percorrida em de até , e uma componente em , que deve ser multiplicada pela distância percorrida em
Por que existe um sinal de negativo? Porque a componente em aponta na direção contrária ao deslocamento.
Beleza, agora vamos analisar o trabalho da força peso.
Passo 4
O trabalho do peso será positivo, já que o peso está agindo de forma a aumentar a velocidade do corpo:
Assim:
E as energias cinéticas? O corpo parte do repouso e atinge uma velocidade ao fim. Sendo assim, a variação de energia cinética será dada por:
Passo 5
Voltando ao início:
Então:
Resolvendo: