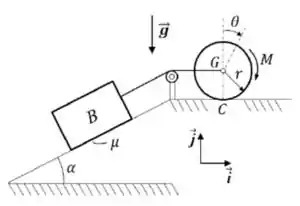
02) Um disco rígido e homogêneo de massa e raio rola sem escorregar sobre um plano horizontal, conforme mostrado na figura. O disco é conectado por um fio ideal a um bloco de massa que escorrega com atrito sobre um plano com inclinação . O sistema parte do repouso quando sob a ação de um momento binário constante. Sabendo que o coeficiente de atrito nas interfaces de contato é , pede-se:

a) A energia cinética do bloco em função da velocidade angular do disco.

b) A energia cinética do disco em função de sua velocidade angular .

c) O trabalho da força normal atuante no bloco em função de .

d) O trabalho da força de atrito atuante no bloco em função de .

e) O trabalho da força peso atuante no bloco em função de .

f) O trabalho da força normal atuante no disco em função de .

g) O trabalho da força de atrito atuante no disco em função de .

h) O trabalho da força peso atuante no disco em função de .

i) O trabalho do momento binário atuante no disco em função de .

j) A velocidade angular do disco em função de .

k) A aceleração angular do disco.

b) Nesse item devemos calcular a energia cinética do disco.

E a pergunta que não quer calar: a rotação vai influenciar em algo na energia cinética?

Hahaha, sim. Com certeza! Sempre que temos um corpo que translada e rotaciona, a energia cinética é dada por:

Lembra que o momento de inércia do disco vale:

Além disso, já vimos que:

Substituindo esses dados, vem:

Logo:

Bouaa! Matamos mais um item 😊

c) Nesse item devemos determinar o trabalho da força normal atuando no bloco.

Mas pô, não precisa nem esquentar a cabeça com esse item, como a força normal é sempre perpendicular ao deslocamento sabemos que o seu trabalho é sempre nulo!

Portanto:

d) Agora devemos determinar o trabalho da força de atrito em função do ângulo de giro do disco.

Das equações da cinemática para um movimento circular, sabemos que:

Só que, pelo vínculo geométrico, o bloco e o disco andam as mesmas distâncias. Assim:

Como o trabalho vale:

Temos:

Mas, como calcular a força de atrito?

Precisamos desenhar o diagrama de forças do bloco. Sabendo que atuam o peso, a normal, a tração e a força de atrito, temos:

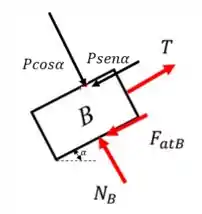
Daí, como o bloco está sempre apoiado no plano inclinado, podemos afirmar que a resultante na direção perpendicular à superfície é nula. Logo:

Sabendo que:

Vem:

Como ela é contra o movimento, seu trabalho é negativo. Substituindo em , vem:

Prontinho 😊

e) Devemos calcular o trabalho da força peso atuando no bloco.

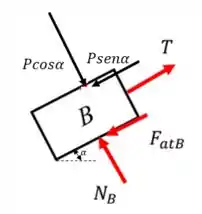
Pelo diagrama de forças do bloco, sabemos que o Peso possui:

- Uma componente perpendicular ao deslocamento , que não realizará trabalho;

- Uma componente no sentido oposto ao deslocamento , que realizará um trabalho negativo.

Portanto, vem:

Do item anterior, sabemos que:

Logo:

Show!

f) Mais um item de graça pra gente 😊

A questão pede pra determinar o trabalho da força normal atuante no disco. Mas, como já vimos, o trabalho da força normal é sempre nulo! Logo:

Fooi!!

g) Aqui devemos calcular o trabalho da força de atrito atuante no disco.

E aí, pergunta malandra agora, será que é só fazer ?

Nãooo hahaha, tem uma pegadinha nesse item. Sabe quando ele fala que o disco rola sem escorregar?

Então, isso significa que a velocidade do ponto de contato do disco na superfície está sempre com . Assim, é como se ele não estivesse sofrendo nenhum deslocamento a cada instante de tempo. Ou seja, temos uma força atuando, a força de atrito, mas não há deslocamento onde ela atua. Logo:

Interessante né? Vamo pro próximo 😊

h) O item nos pede para calcular o trabalho da força peso atuante no disco.

Basicamente, o trabalho da força peso é dado por:

Só que o nosso disco rola sob uma superfície plana horizontalmente, ou seja, não tem variação de altura.

Assim, temos também:

Perfeito!

i) Pra finalizar essa onda de cálculo de trabalho, devemos determinar o trabalho do momento binário atuante no disco. Vocês lembram como podemos calcular o trabalho de um momento?

Haha, bora rever agora pra não esquecer nunca mais. É só fazer:

Onde é o tanto que o disco girou enquanto o momento atuava. Pra essa questão o trabalho vai ser exatamente esse.

Prontinho 😊

Calma lá, já estamos acabando haha.

j) Devemos determinar a velocidade angular do disco, , em função de .

Bora ser esperto galera, todos esses itens mandando calcular trabalho não são à toa. Vamos abordar esse item por energia. Como temos forças conservativas e não conservativas misturadas, uma boa ideia é aplicar o Teorema da Energia Cinética. Assim, temos:

Logo:

O legal é que já determinamos todas essas variáveis nos itens anteriores. Daí, substituindo vem:

Colocando em evidência, temos:

Isolando , vem:

Logo:

Só deixando mais bonito, ficamos com:

Boa, falta só mais um itemm!

k) Pra finalizar, devemos determinar a aceleração angular do disco.

Lembra que:

E que:

Então é isso que vamos tentar usar. Do item anterior, temos:

Se derivarmos os dois lados da equação em relação ao tempo, temos:

Massa! Agora é só isolar :

AEEEE, terminamos!!! Bouaa galera.

Aproveita pra beber uma água, dar uma respirada, e depois já volta com tudoo. Tamo junto!