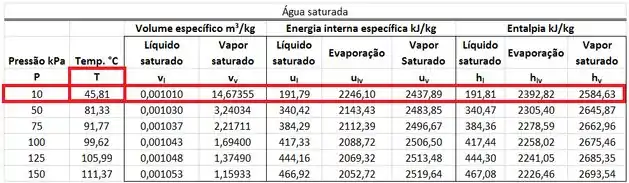
A Fig. P6.53 mostra o esquema de uma pequena turbina a vapor d’água que produz uma potência de operando em carga parcial. Nesta condição, a vazão de vapor é , a pressão e a temperaturana seção são, respectivamente, iguais a e e o vapor é estrangulado até antes de entrar na turbina. Sabendo que a pressão de saída da turbina é , determine o título; ou a temperatura, se o vapor estiver superaquecido; da água na seção de saída da turbina.
Passo 1
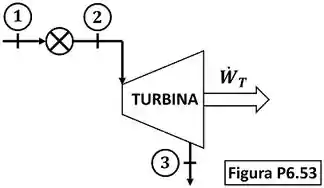
Essa questão envolve dois equipamentos: a restrição que está entre os estados e da água e a turbina que está entre os estados e da água. O enunciado pede que a gente encontre o valor do título ou a temperatura da água que está saindo da turbina no estado . A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esses valores.
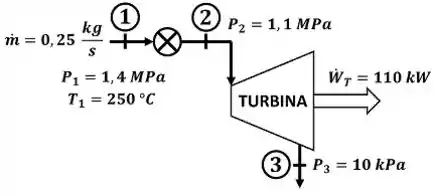
é a temperatura do vapor d’água entrando na restrição e é a temperatura da água saindo da turbina. é a pressão do vapor d’água entrando na restrição, é a pressão da água entrando na turbina e é a pressão da água saindo da turbina. é a vazão mássica de água que passa pela turbina e pela restrição. é a potência gerada pela turbina. é o título da água saindo da turbina.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular e na próxima etapa.
Passo 2
Para encontrar as propriedades do estado e nós precisamos determinar o estado da água saindo da turbina. Nós fazemos isso descobrindo o valor de duas propriedades da água nesse estado . Um já foi dado. É a pressão que vale . O outro valor que podemos descobrir é a entalpia especifica da água saindo da turbina. Ela é encontrada através da equação da primeira lei para turbina que está abaixo.
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor de . é encontrado através da equação da primeira lei para restrições mostrada abaixo.
Ou seja, o valor de é igual ao valor de . No próximo passo vamos aprender a encontrar o valor de .
Passo 3
A entalpia específica do vapor entrando na restrição para uma pressão de e uma temperatura de só pode ser encontrada na tabela de vapor superaquecido. Ela está na mesma linha que a temperatura de e na mesma coluna que .
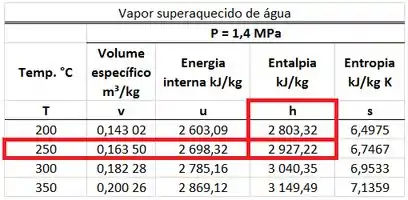
Isso quer dizer que:
Com esse valor encontramos . Mas como podemos encontrar ou através da entalpia especifica ?
Veremos isso no próximo passo!
Passo 4
Atenção! A água que sai de uma turbina a vapor NUNCA será um líquido comprimido, porque isso danificaria o equipamento. Ou seja, a água do estado (que esta saindo da turbina) só pode estar em duas fases: ou saturada ou vapor superaquecido. Se ela for saturada, o exercício pede que a gente calcule e , se ela for um vapor superaquecido, o exercício pede .
Para decidir se a água do estado é saturada ou não, precisamos encontrar o valor de entalpia do vapor saturado a . Se a entalpia for maior que , então a água é um vapor superaquecido. Se a entalpia for menor que , então ela está saturada. Caso ela esteja saturada, calculamos o título através da fórmula abaixo.
onde é a entalpia da água líquida saturada .
A temperatura da água saturada a é encontrada em uma tabela de saturação da água na mesma linha que a pressão de e na mesma coluna que .
e são encontrados na tabela de saturação da água na mesma linha que a pressão de .
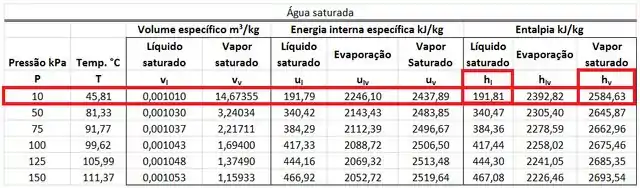
Caso a água seja um vapor superaquecido, a temperatura é encontrada em uma tabela de vapor superaquecido para pressão de e entalpia de .
Sabendo disso, podemos iniciar as contas.
Passo 5
A entalpia é calculada abaixo.
Comparando o valor acima com a entalpia do vapor saturado a , percebemos que é menor! Isso significa que a água que sai da turbina no estado está saturada e precisamos encontrar com a fórmula abaixo.
A temperatura é encontrada na tabela de saturação da água abaixo.