Uma turbina é alimentada com de vapor a e . O vapor é descarregado da turbina como vapor saturado a . Sabendo que a velocidade na seção de alimentação da turbina é igual a e que a velocidade na seção de descarga é pequena, determine o trabalho específico e a potência gerada pela turbina.
Passo 1
A questão pede que a gente calcule o valor da taxa de trabalho (potência) realizado pela turbina e também pede que a gente calcule a divisão entra a potência e a vazão mássica de vapor que é chamada de trabalho específico. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esses valores.
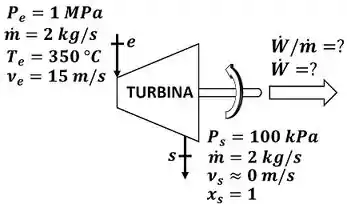
é a temperatura do vapor entrando na turbina e é a temperatura do vapor saindo da turbina. é a pressão do vapor entrando na turbina e é a pressão do vapor saindo da turbina. é a vazão mássica de vapor que passa pela turbina. Ela é igual na entrada e na saída, porque a turbina está funcionando em regime permanente.

é a velocidade do vapor entrando na turbina e é a velocidade do vapor saindo da turbina.
é o título do vapor saindo da turbina. Como o vapor saindo da turbina está saturado, o título vale .
Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular e na próxima etapa.
Passo 2
Calculamos e através da equação da primeira lei da turbina em regime permanente. Mas tenha ATENÇÃO! O enunciado diz que o valor da velocidade de entrada do vapor vale . Ou seja, precisamos levar em conta a energia cinética do vapor na entrada da turbina. Como o enunciado diz que é pequena, podemos desprezar a energia cinética do vapor na saída da turbina.
Na fórmula acima, vemos que o termo da energia cinética está dividido por . Isso é necessário para passar a unidade desse termo de para .
Além disso, podemos ver que para calcular o valor de , precisamos encontrar os valores de e . No próximo passo veremos como fazer isso.

Despois de calcular , calculamos o trabalho específico , dividindo por pela vazão mássica .
Passo 3
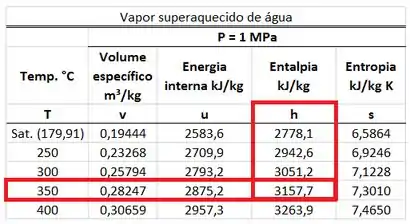
A entalpia específica do vapor entrando na turbina para uma pressão de e uma temperatura de só pode ser encontrada na tabela de vapor superaquecido. Ela está na mesma linha que a temperatura de e na mesma coluna que .
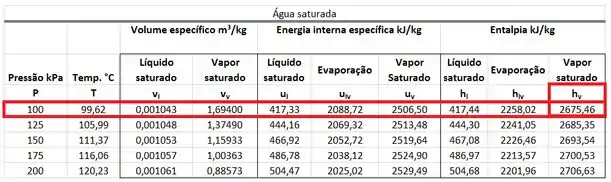
Como o vapor saindo da turbina está saturado, encontramos o valor de na tabela de saturação da água. Ela está na mesma linha que a pressão de e na mesma coluna que a entalpia do vapor saturado .
Com esses dois valores já podemos partir para as contas!
Passo 4
Dividindo esse valor pela vazão mássica, encontramos o trabalho específico realizado pela turbina.