Uma turbina pequena e de alta velocidade é alimentada com ar comprimido e produz uma potência de . O estado na seção de entrada da turbina é e e o estado na seção de saída é e . Admitindo que as velocidades sejam baixas e que a turbina seja adiabática, determine a vazão de ar necessária na turbina.
Passo 1
A questão pede que a gente calcule o valor da vazão mássica de ar que passa pela turbina. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
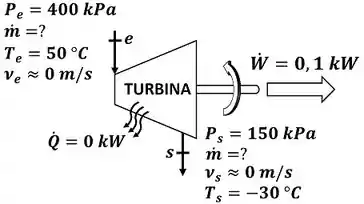
é a temperatura do ar entrando na turbina e é a temperatura do ar saindo da turbina. é a pressão do ar entrando na turbina e é a pressão do ar saindo da turbina. é a velocidade do ar entrando na turbina e é a velocidade do ar saindo da turbina. é a potência gerada pela turbina. é a taxa de calor trocada entre a turbina e o ambiente.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular na próxima etapa.
Passo 2
Calculamos através da equação da primeira lei da turbina em regime permanente. Como o enunciado diz que as velocidades e são muito pequenas, podemos tirar os termos de energia cinética do ar da equação. Além disso, o enunciado diz que o processo de expansão do ar é adiabático. Por isso, também tiramos o termo de taxa de troca de calor da equação.
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor da diferença entre as entalpias específicas do ar e .
Como o ar pode ser considerado um gás perfeito, pode ser calculado através da fórmula abaixo.
onde é o calor específico do ar a pressão constante. Ele vale:
Atenção! As duas temperaturas presentes nessa fórmula tem que estar em kelvin . No entanto, estamos apenas interessados nas diferenças de temperaturas. Além disso, a diferença de temperatura em kelvin é igual à diferença de temperatura em grau Celsius . Por isso, podemos substituir os valores das temperaturas em grau Celsius na fórmula!
Substituindo essa fórmula na equação da primeira lei, encontramos:
Sabendo disso, podemos iniciar as contas!