Hélio é estrangulado de e até a pressão de . Os diâmetros do tubo de alimentação e descarga são tais que as velocidades de saída e entrada são iguais. Determine a temperatura de saída do hélio e a razão entre os diâmetros dos tubos.
Passo 1
O primeiro passo para resolver essa questão é saber por qual equipamento o hélio está passando para diminuir sua pressão. A resposta para isso é encontrada no enunciado, quando ele diz que o hélio é “estrangulado”. Quando o texto diz que uma substância está sendo estrangulada, ele quer dizer que ela está passando por uma restrição!

O exercício quer saber a temperatura do hélio saindo da restrição e a relação entre os diâmetros do tubo de entrada e saída que estão conectados à restrição. Para encontrar esses valores, temos que entender todos os dados que o enunciado nos informa. A figura abaixo mostra esses dados.
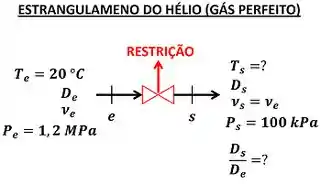
é a temperatura do hélio entrando na restrição e é a temperatura do hélio saindo da restrição. é a pressão do hélio entrando na restrição e é a pressão do hélio saindo da restrição. é a velocidade do hélio entrando na restrição e é a velocidade do hélio saindo da restrição. é o diâmetro do tubo por onde o hélio passa para entrar na restrição e é o diâmetro do tubo por onde o hélio passa quando sai da restrição.

Agora que sabemos disso tudo vamos aprender a calcular a temperatura e a relação nos próximos passos!
Passo 2
A gente encontra através equação da primeira lei para restrições que está abaixo.
Ela diz que a entalpia específica do gás hélio entrando na restrição é igual à entalpia específica do gás hélio saindo sa restrição .
Quando o gás hélio aparece em um exercício de termodinâmica, ele geralmente é um gás perfeito. Para um gás perfeito, a função de cálculo das entalpias só depende da temperatura. Logo, para esse exercício, as entalpias e dependem só das temperaturas.
Para as duas entalpias serem iguais, o valor das temperaturas precisam ser iguais. Logo:
Agora vamos aprender a calcular !
Passo 3
A razão é encontrada através da equação de conservação de massa da restrição em regime permanente. Ela diz que a vazão mássica de entrada é igual à vazão mássica de saída . É importante lembrar também que essas vazões são iguais ao produto entra massa específica do hélio , velocidade do hélio e área de passagem do hélio .
onde e são os volumes específicos do hélio entrando e saindo da restrição respectivamente.
No entanto, o enunciado diz que as duas velocidades e devem ser iguais. Logo, elas podem ser cortadas dos dois lados da equação acima, assim como o e o !
Além disso, como o hélio é um gás perfeito, os volumes específicos e podem ser calculados pela equação de gás perfeito.
Como as duas temperatura são iguais, elas são cortadas dos dois lados da equação!
Substituindo isso na equação de conservação de massa, achamos:
Agora que temos fórmulas para calcular todos os valores que queremos, vamos iniciar as contas!
Passo 4
Antes de usar o valor de na fómula ele precisa estar na mesma unidade de .