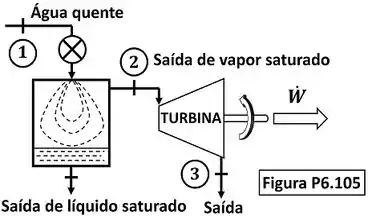
Propõe-se usar um suprimento geotérmico de água quente para acionar uma turbina a vapor d’água utilizando o dispositivo esquematizado na figura P6.105. Água a alta pressão, e , é estrangulada, num evaporador instantâneo adiabático, de modo a obter líquido e vapor a pressão de . O líquido sai pela parte inferior do evaporador, enquanto o vapor é retirado para alimentar a turbina. O vapor sai da turbina a e com título igual a . Sabendo que a turbina produz uma potência de , qual é a vazão necessária de água quente, em , que deve ser fornecida pela fonte geotérmica?
Passo 1
O enunciado pode assustar por conta da quantidade de informação, mas pode relaxar! Essa questão envolve dois equipamentos que conhecemos bem: a restrição que estrangula o vapor e a turbina que gera potência!

A questão quer que a gente calcule a vazão de água quente que entra na restrição. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
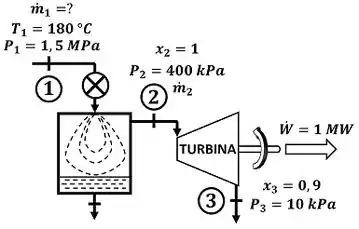
é a temperatura da água entrando na restrição. é a pressão da água entrando na restrição, é a pressão da água entando na turbina e é a pressão da água saindo da turbina. é a vazão mássica de água entrando na restrição e é a vazão mássica de água passando pela turbina. é o título da água entrando na turbina. Ele vale , porque a figura mostra que esse estado é de vapor saturado. é o título da água saindo da turbina.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular próxima etapa.
Passo 2
Para a gente conseguir encontrar a vazão de água quente , a gente precisa primeiro calcular . é calculado através da primeira lei para regime permanente aplicada à turbina. A corrente de água está entrando na turbina e a corrente de água está saindo dela. A equação da primeira lei se encontra abaixo.
Como a turbina está em regime permanente, toda massa que entra tem que sair. Por isso, a vazão de água que entra é igual à vazão de água que sai .
A fórmula acima mostra que para calcular , precisamos encontrar os valores das entalpias específicas e . Por isso, no próximo passo vamos aprender a calcular esses valores.
Passo 3
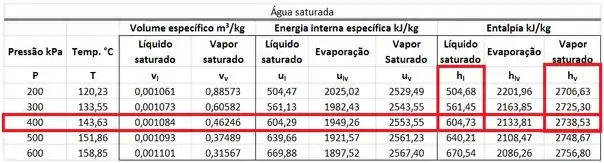
O valor de pode ser encontrado na tabela de saturação da água. Ele está na mesma linha que a pressão de e na mesma coluna que a entalpia específica do vapor saturado .
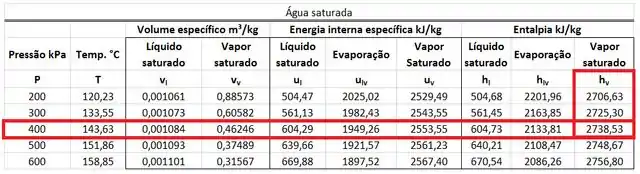
O valor de também pode ser encontrado na tabela de saturação da água. Ele é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . A fórmula dele se encontra abaixo.
está na mesma linha que a pressão de na mesma coluna que da tabela. está na mesma linha que a pressão de na mesma coluna que da tabela.
O próximo passo é a primeira etapa para aprender a calcular a vazão mássica de água quente que a questão pede.
Passo 4
Para descobrir quanto vale temos que descobrir quanto vale o título da água que sai da restrição. Faremos isso agora!

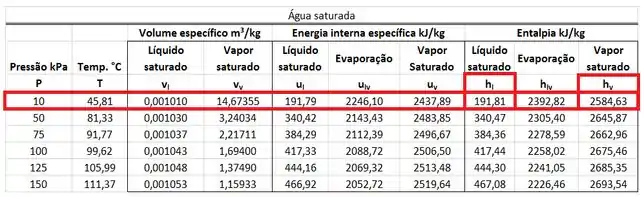
A figura da questão mostra que a água que sai da restrição é uma mistura de líquido saturada a e vapor saturado a . Por isso, a entalpia dessa corrente de água é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . A fórmula dessa entalpia está abaixo.
está na mesma linha que a pressão de na mesma coluna que da tabela de saturação. está na mesma linha que a pressão de na mesma coluna que da tabela de saturação.
Se a gente reorganizar essa equação, a gente consegue criar uma fórmula para o título .
A gente consegue encontrar a entalpia específica aplicando a equação da primeira lei na restrição. Essa equação diz que é igual à entalpia específica da corrente de água quente.
A corrente de água é um líquido comprimido porque a sua pressão é maior que a pressão de saturação a . Por isso, a gente teria que ver o valor da entalpia específica dessa corrente na tabela de líquido comprimido. No entanto, geralmente não temos tabelas de líquido comprimido para uma pressão tão baixa.

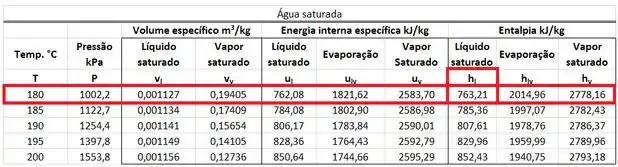
Para resolver esse problema, podemos considerar igual a entalpia de líquido saturado a . Esse valor está na mesma linha que a temperatura de e na mesma coluna que .
Agora que aprendemos a calcular o título da água que sai da restrição, vamos para a útlima etapa de cálculo de .
Passo 5
pode ser calculado de outro jeito. Saber isso é fundamental para calcular . é a massa de vapor d’água presente na corrente dividida pela massa total de água presente na corrente. A massa de vapor que escoa a cada segundo pela saída da restrição é igual à vazão . A massa total que escoa pela saída da restrição a cada segundo é igual à . Logo, é igual a:
Reorgazinando essa fórmula, encontramos uma fórmula para .
Depois de entender tudo isso, podemos iniciar as contas!
Passo 6
Primeiro vamos determinar quanto vale .
Com esse valor, podemos achar . Mas ates temos que converter a unidade de de para .
O próximo passo é achar o valor de .
Por fim, podemos calcular .
Ainda não acabou! O enunciado pede que a gente dê o resultado em . Para converter de para , temos que multiplicar por .