Vapor d’água saturado a é estrangulado, numa válvula parcialmente aberta, até a pressão de . Admitindo que o processo seja adiabático e que as variações de energia cinética e potencial são desprezíveis, determine a temperatura do vapor após o estrangulamento.
Passo 1
O enunciado diz que o vapor d’água saturado é estrangulado numa válvula parcialmente. Essa válvula é uma restrição ao escoamento da água. O exercício quer saber a temperatura da água saindo da restrição. Para encontrar ess valor, temos que entender todos os dados que o enunciado nos informa. A figura abaixo mostra esses dados.
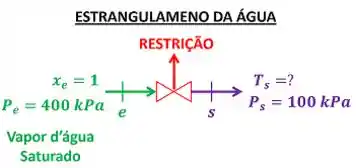
é a pressão da água entrando na restrição e é a pressão da água saindo da restrição. é o título da água entrando na restrição. Como a água que entra na restrição é um vapor saturado, o seu título é igual a .
Agora que sabemos disso tudo vamos aprender a calcular a temperatura nos próximos passos!
Passo 2
A gente encontra através equação da primeira lei para restrições que está abaixo.
Nós só podemos saber primeiro qual é o valor da entalpia específica , porque apenas o estado da água entrando na restrição é que está definido pelo valor de duas propriedades ( e ).
pode ser encontrada em uma tabela de saturação da água. Esse valor está na mesma linha da pressão de e na mesma coluna da entalpia específica do vapor saturado .
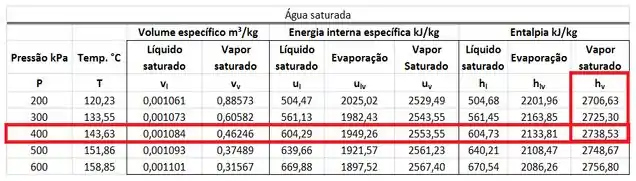
Como é igual a , vale:
Isso significa que nós determinamos já determinamos o estado de saída da água, porque temos o valor de duas propriedades: a sua entalpia e a sua pressão .
No próximo passo vamos descobrir a primeira etapa para encontrar a temperatura a partir dessa nova informação.
Passo 3
Se for maior que a entalpia específica do vapor saturado a , a água está na forma de vapor superaquecido.
Se for menor que a entalpia específica do líquido saturado a , a água está na forma de líquido comprimido.
Se for maior que a entalpia específica do líquido saturado a e menor que a entalpia específica do vapor saturado a , a água está saturada.
Os valores de e são achados na tabela de saturação da água para uma pressão de . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado .
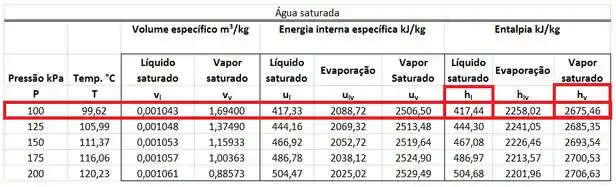
Como é maior que , a água da saída da restrição é um vapor superaquecido e teremos que achar o valor de através de uma tabela de vapor superaquecido. Deixaremos essa parte para o próximo passo.
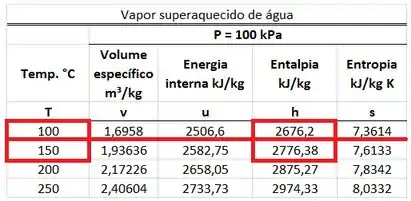
Passo 4
A tabela de vapor superaquecido a se encontra abaixo. Nessa tabela não existe o valor de temperatura da água, quando sua entalpia específica vale tanto quanto . Só temos a temperatura para uma entalpia menor de e uma temperatura para uma entalpia maior de . A entalpia que temos está no meio dessas duas. Por isso, vamos ter que interpolar o valor de .