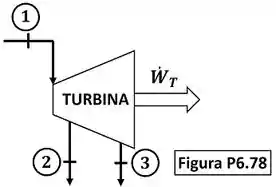
Uma turbina é alimentada com de vapor d’água a e . Num estágio intermediário, onde e , é realizada a extração de (ver Fig. P6.78). Na seção final de descarga, a pressão e o título são respectivamente, iguais a e . Admitindo que a turbina seja adiabática e que as variações de energia cinética e potencial sejam desprezíveis, determine a potência da turbina.
Passo 1
Esse é um exercício de turbina diferente, porque essa turbina, ao contrário das turbinas comuns, têm duas vazões de saída! A questão pede que a gente calcule a potência gerada pela turbina. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
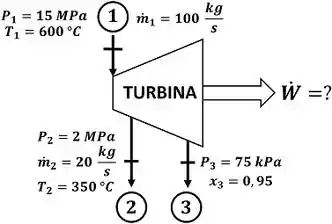
é a temperatura do vapor d’água entrando na turbina, é a temperatura da água saindo da turbina pela saída intermediária. é a pressão do vapor d’água entrando na turbina, é a pressão da água saindo da turbina pela saída intermediária e é a pressão da água saindo da turbina pela saída final. é a vazão mássica de água entrando na turbina e é a vazão mássica de água saindo da turbina pela saída intermediária. é o título da água saindo da turbina pela saída final.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular próxima etapa.
Passo 2
Calculamos através da primeira lei da termodinâmica aplicada a uma turbina que funciona em regume permanente. Mas cuidado. Esse caso é diferente do que estamos acostumados. Ele inclui mais um termo de entalpia específica!
onde , e são as entalpias específicas das correntes de água , e .
Os termos das energias cinética e potencial e da taxa de troca de calor não estão presentes na equação, porque o enunciado disse que eles são desprezíveis.
pode ser calculado através da equação de conservação de massa.
Podemos ver pela primeira lei que precisamos determinar os valores de , e para calcular . Faremos isso na próxima etapa!
Passo 3
A entalpia da corrente de água só pode ser encontrada na tabela de vapor superaquecido para uma pressão de e . Ela está na mesma linha que a temperatura de e na mesma coluna que .
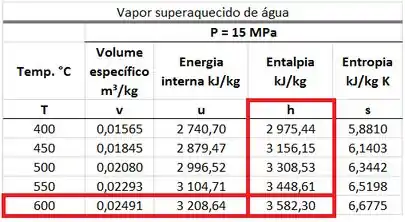
A entalpia da corrente de água só pode ser encontrada na tabela de vapor superaquecido para uma pressão de e . Ela está na mesma linha que a temperatura de e na mesma coluna que .
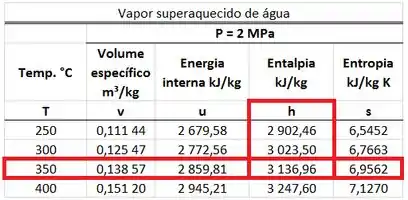
A entalpia da corrente de água só pode ser encontrada na tabela de água saturada, porque ela tem um título. Ela é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . Para calcular , precisamos da fórmula abaixo.
está na mesma linha que a pressão de na mesma coluna que da tabela. está na mesma linha que a pressão de na mesma coluna que da tabela.
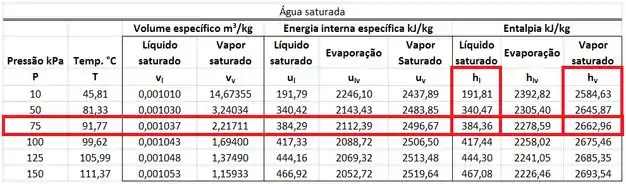
Com todos esses valores em mãos, podemos finalmente iniciar as contas.
Passo 4
Vamos começar os cálculos, determinando quanto vale .
Agora vamos determinar o valor de .
Agora sim podemos calcular .