Uma barra de aço () e uma barra de alumínio () são unidas para formar a barra composta mostrada na figura. Determine a tensão máxima, no alumínio e no aço, quando a barra é flexionada em torno do eixo horizontal, com .
Passo 1
O que está acontecendo?
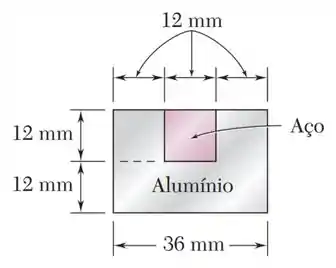
A viga composta da figura é feita de aço (com um módulo de elasticidade ) e alumínio (com um módulo de elasticidade ).
Um momento em torno do eixo horizontal é aplicado nessa viga, gerando tensões normais de flexão nela.
Lembrando que, como a viga é composta, precisamos usar o método da seção transformada para calcular essas tensões nela.
E o que é que o exercício quer?
Ele quer saber as tensões máximas no alumínio e no aço nessa viga.
Para tanto, vamos ter que:
1. Transformar a seção composta em uma seção transformada feita toda de um material;
Aqui, escolhendo por transformar a parte de aço em uma parte equivalente de alumínio, vamos ter que definir um fator de transformação para podermos calcular a largura da parte equivalente.
2. Calcular as propriedades geométricas ( e ) para essa seção transformada;
& 3. Calcular as tensões no alumínio e no aço usando a fórmula da flexão, sabendo que as tensões no aço devem ser multiplicadas por , uma vez que ele teve sua largura transformada.
Ou seja, vamos calcular as tensões no alumínio através da fórmula:
E as tensões no aço através da fórmula:
Passo 2
Então vamos começar pelo primeiro passo, que é a:
![]()
Começamos definindo o fator de transformação:
E calculamos o valor da largura da parte de alumínio equivalente à parte de aço:
Aqui, substituindo e vendo na figura do exercício que a parte de aço tem uma largura original , vamos ter que:
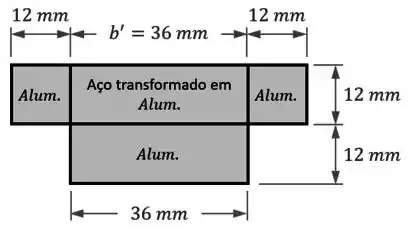
Dessa forma, a nossa seção transformada fica assim:
Passo 3
Agora, vamos seguir com o cálculo das:
![]()
Primeiro, devemos encontrar a posição da linha neutra para essa seção transformada.
Então vamos lá!
Começamos separando a nossa seção transformada em elementos numerados e definimos a base da seção como a posição :
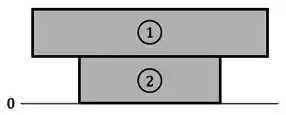
Feito isso, preenchemos em uma tabela os valores das áreas e das posições dos centros de cada elemento, aproveitando as dimensões do desenho feito ao final do passo anterior:

Nessa tabela, ainda preenchemos na última coluna o valor do produto para cada elemento e na última linha o valor dos somatórios das áreas e dos produtos .
Assim, conseguimos calcular a posição da linha neutra:
Passo 4
Calculada a posição da linha neutra, podemos agora calcular o momento de inércia da área para a seção transformada.
Para tanto, começamos calculando o momento de inércia da área de cada elemento, aproveitando as dimensões de cada elemento indicadas nos desenhos anteriores.
Para o elemento , que é retangular de base e altura , vamos ter:
Já para o elemento , retangular de base e altura , temos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
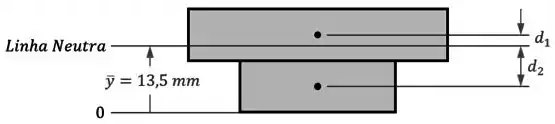
O centro do elemento está a uma altura de , então sua distância vai dar:
Já o centro do elemento está a uma altura de , então sua distância vai dar:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transformada como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Passo 5
Finalmente, podemos fazer o:
![]()
Aqui, devemos primeiro identificar as posições em relação à linha neutra dos pontos em que queremos calcular as tensões no alumínio e no aço.
Queremos calcular as tensões máximas no alumínio e no aço, então queremos usar as posições máximas em termos absolutos para o alumínio e para o aço.
Olhando para os desenhos anteriores que fizemos para a nossa seção, vemos que:
- Os pontos do alumínio mais distantes da linha neutra ficam na borda inferior da viga, onde ;
- Enquanto que os pontos do aço mais distantes da linha neutra ficam na borda superior da viga, onde .
Então, aplicando a fórmula da flexão para o cálculo da tensão máxima no alumínio, vamos ter:
Substituindo os valores abaixo, sempre em função das unidades e :
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Vamos ter que:
Calculando isso e sabendo que é o mesmo que , encontramos que:
O que é uma tensão de tração, como demonstrado pelo sinal positivo.
Já para o aço, como ele teve sua largura transformada por um fator de transformação , a sua fórmula da flexão deve ser multiplicada por .
Dessa fórmula, aplicando a fórmula da flexão, multiplicada por , para o cálculo da tensão máxima no aço, vamos ter:
Aí, substituindo os valores, sempre em função de e :
E calculando tudo, vamos encontrar que:
O que é uma tensão de compressão, como demonstrado pelo sinal negativo.
E assim, lembrando que a letra queria saber a tensão máxima no alumínio e a letra queria saber a tensão máxima no aço, terminamos o nosso exercício: