uma peça de madeira foi reforçada com uma barra de ferro como mostras a figura. Usando seus conhecimentos sobre vigas compostas e sabendo que o modulo de elasticidade da madeira é dado por e determine a tensão na extremidade do aço e na interface aço madeira. O momento fletor que age sobe essa peça é de 15KN.m. observe os eixos usados.
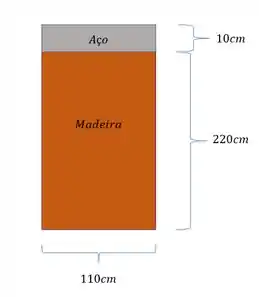
Passo 1
Para resolvermos esse tipo de questão, temos que ter na mente duas situações muito importante. A primeira é saber que algum dos materiais terá que ser transformado em um equivalente do outro. E que para fazer essa equivalência precisamos calcular o valor de n e b’.
Executado esses dois primeiros passos, todo o resto se torna mais fácil pois usamos as fórmulas de flexão que já conhecemos.
Então vamos lá, sabemos que o cálculo de n depende dos materiais que serão transformados e dos módulos de elasticidade.
A fórmula é
Por conveniência eu sempre escolho transformar o material de módulo de elasticidade menor, nesse caso a madeira, dessa forma o nosso valor de n será
Para determinar b’ é simples, é só multiplicar a largura do material que iremos transformar pelo valor de n que determinamos antes, então
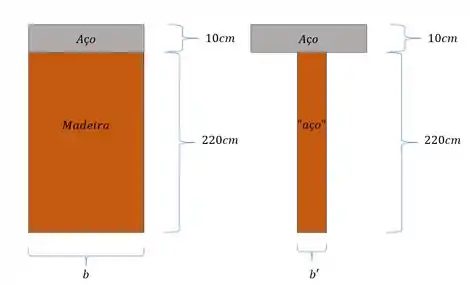
Agora temos um perfil T para resolvermos
Passo 2
Agora que já sabemos como é nossa seção equivalente, devemos saber algumas coisas sobre como iremos calcular as nossas tensões normais
Primeiro temos que saber que a fórmula entre as tensões na parte intacta e na parte transformada são calculadas por fórmulas diferentes, e as fórmulas são
Ou seja, na parte transformada consideramos para o cálculo da tensão o valor de n.
Outro ponto importante é se atentar para o valor de Y quando for calcular tanto a seção intacta quanto a transformada. Agora que já sabemos isso vamos ao cálculo.
Passo 3
Sabemos que o valor do momento é facilmente adquirido, além do mais ele já foi dado no enunciado
Com relação ao valor de Y teremos que descobrir a posição da linha neutra, para isso teremos que fazer o nosso passo a passo
Primeiro determinamos a origem do nosso sistema

Em seguida descobrimos quanto vale a área e a distância do centroide de cada elemento até a nossa origem.
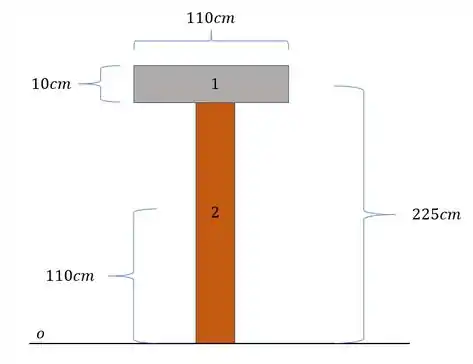
Dessa forma descobrimos facilmente que
Definimos assim a nossa linha neutra
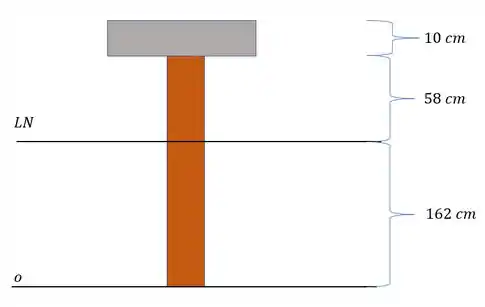
Com relação ao valor de Y teremos que
Para o trecho acima da linha neutra
Lembrando que o negativo existe pelo fato de arbitrarmos y negativo pra cima
Para o trecho abaixo da linha neutra
Também já calculamos no primeiro passo o valor de n, logo
Agora só falta o momento de inércia
Passo 4
Para o cálculo do momento de inércia teremos que usar de novo o nosso passo a passo. Sabemos que para calcularmos momentos de inercia precisamos determinar 3 coisas. As áreas de cada elemento, a distância do centroide de cada elemento até a linha neutra e por fim o momento de inercia de cada elemento. Como os elementos são retangulares, teremos que o momento de inercia deles é
A figura abaixo representa as distâncias dos centroides de cada elemento até a linha neutra
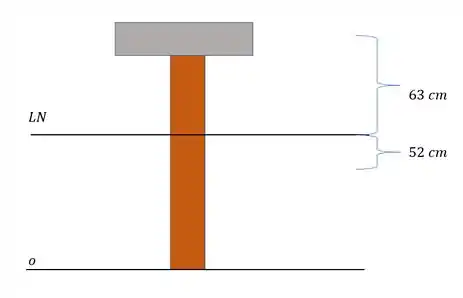
E nessa imagem temos as medidas para calcularmos os momentos de inercia
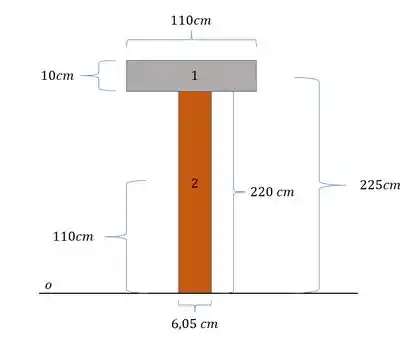
Calculando o momento de inercia de cada elemento teremos que
E no passo anterior já tínhamos determinado o valor das áreas
Agora que já temos todos os valores, bata calcularmos o momento de inercia para a fórmula
Passo 5
Agora que já temos todos os valores basta calcularmos as tensões
Para o caso intacto, temos o ponto extremo do aço e o ponto interface aço madeira, então calcularemos duas tensões.
Caso extremidade do aço
Caso interface aço-madeira
Passo 6
Caso interface madeira aço (caso transformado)
Substituindo
Caso madeira extremo
Substituindo
Resposta
extremidade do aço
interface aço-madeira
Caso interface madeira aço (caso transformado)
Caso madeira extremidade