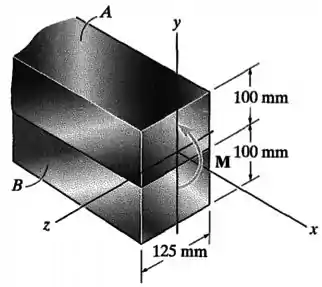
A viga composta é feita de aço A-36 e latão vermelho C83400 e tem a seção transversal mostrada na figura. Se for submetida a um momento , determine a tensão máxima no latão e no aço. Determine também a tensão em cada material na junção entre eles.
Dados: , .
Passo 1
O que está acontecendo?
Nesse exercício, nós temos uma viga composta por uma parte superior de aço (com módulo de elasticidade ) e uma parte inferior de latão (com módulo de elasticidade ).
Além disso, tanto a parte de aço quanto a parte de latão possuem uma altura e uma largura ou base .
A viga é submetida a um momento , que vai gerar tensões normais de flexão nela.
Mas como ela é composta, não podemos usar diretamente a fórmula da flexão nela.
Precisamos primeiro usar o método da seção transformada (que também pode ter infinitos outros nomes como método da área equivalente ou método da largura equivalente).
De acordo com esse método, se escolhermos transformar a parte de latão em uma parte equivalente de aço, por exemplo, devemos definir um fator de transformação :
Para depois calcular a largura da parte de aço equivalente à parte de latão:
Dessa forma, vamos conseguir definir uma seção transformada ou equivalente feita toda de aço:
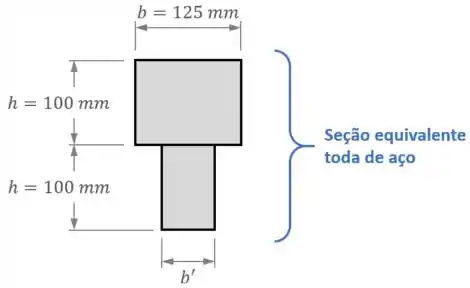
Assim, para essa seção transformada, será possível calcular as tensões normais de flexão normalmente, através dos passos que já conhecemos:
- Determinação da posição da linha neutra;
- Determinação do momento de inércia da área para a seção;
- E finalmente, aplicação da fórmula da flexão .
Aí, ao final, as tensões no aço podem ser calculadas diretamente pela fórmula da flexão, enquanto que as tensões no latão, que teve sua largura transformada, devem ser multiplicadas por .
Ou seja:
E o que é que o exercício quer?
Ele quer saber a tensão máxima no latão e no aço, que vão ocorrer nas bordas inferior e superior da seção.
Além disso, ele também que a gente determine as tensões no latão e no aço no ponto em que há a interface entre esses materiais.
Então, para resolver o exercício, vamos:
- Transformar a seção composta em uma seção transformada feita toda de aço;
- Calcular as propriedades geométricas ( e ) para essa seção transformada;
- Identificar as posições em relação à linha neutra das bordas inferior e superior da seção, além da posição da borda entre os materiais;
- E, finalmente, aplicar a fórmula para determinar as tensões no aço e a fórmula para determinar as tensões no latão, uma vez que o latão teve sua largura transformada anteriormente.
Passo 2
Então vamos lá!
Primeiro, vamos fazer a:

Para tanto, começamos definindo o fator de transformação:
Substituindo os valores desses módulos de elasticidade de acordo com os dados fornecidos pelo exercício, vamos ter que:
Agora, podemos calcular o valor da largura da parte de aço equivalente à parte de latão:
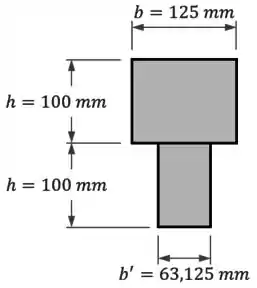
Substituindo e a largura original da parte de latão, , temos:
Dessa forma, a nossa seção transformada fica assim:
Passo 3
Agora, podemos determinas as:
![]()
Primeiro, determinamos a posição da linha neutra.
Para tanto, começamos numerando os elementos da seção transformada e estabelecendo a base da seção como a posição :
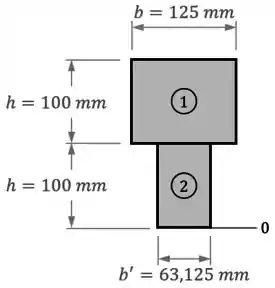
Com isso, podemos preencher uma tabela com os valores das áreas e das posições dos centros de cada elemento:
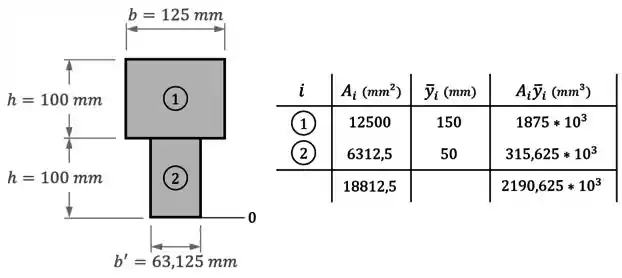
Sendo que, ainda nessa tabela, também preenchemos na coluna final os valores dos produtos para cada elemento e na linha final os valores dos somatórios das áreas e dos produtos .
Assim, podemos finalmente calcular a posição da linha neutra:
Passo 4
Depois de termos calculado a posição da linha neutra, calculamos o momento de inércia da área para a seção transformada.
Começamos calculando o momento de inércia da área de cada elemento.
Para o elemento retangular , vamos ter:
Já para o elemento retangular , que tem a base transformada , vamos ter:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
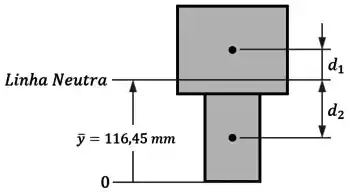
O centro do elemento está a uma altura de , então sua distância vai ser:
Já o centro do elemento está a uma altura de , então sua distância vai ser:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transformada como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Passo 5
Finalmente, podemos fazer o:
![]()
Aqui, devemos primeiro identificar as posições em relação à linha neutra dos pontos em que queremos calcular as tensões no aço e no latão.
Como queremos calcular as tensões nas bordas inferior e superior da seção, e na borda entre os materiais, vamos observar as posições dessas bordas:
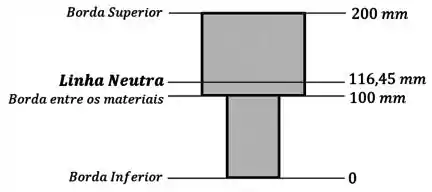
Desse esquema acima, vemos que a borda superior tem uma posição em relação à linha neutra:
Já a borda na junção entre os materiais tem uma posição:
Enquanto que a borda inferior tem uma posição:
Dessa forma, a tensão na borda superior, que vai ser a tensão máxima na região superior ocupada pelo aço, vai ser:
Substituindo todos os valores em função de e :
- ;
- ;
- & ,
- ;
- ;
- e ;
- & ,
Encontramos que:
Simplificando isso, e sabendo que é o mesmo que , temos que:
O que dá:
Já a tensão no aço na região da junção entre os materiais vai ser:
Seguindo os mesmos passos da tensão que acabamos de calcular, mas dessa vez usando , vemos encontrar que:
O que dá:
Agora...
Para as tensões no latão, que teve sua largura transformada pelo fator de transformação , a fórmula da flexão deve ser multiplicada por .
Dessa forma, a tensão na borda inferior, que vai ser a tensão máxima na região inferior ocupada pelo latão, vai ser:
Enquanto que a tensão no latão na região da junção entre os materiais vai ser:
Substituindo nessas equações todos os valores em função de e :
Elas ficam assim:
Daí, calculando tudo e sabendo que é o mesmo que , encontramos que:
E assim terminamos o nosso exercício!
Por fim, na hora de fornecer os resultados, podemos colocar somente os seus valores absolutos e indicar entre parênteses se são tensões de tração ou compressão: