Determine o cortante e o momento em uma seção da viga carregada à direita de .
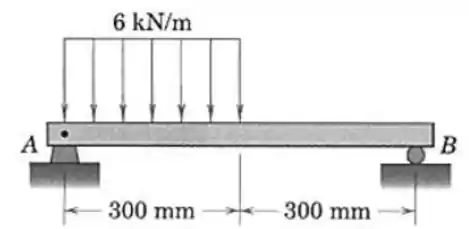
Passo 1
Primeiro temos que achar as reações de apoio e para isso temos que montar o diagrama de corpo livre:
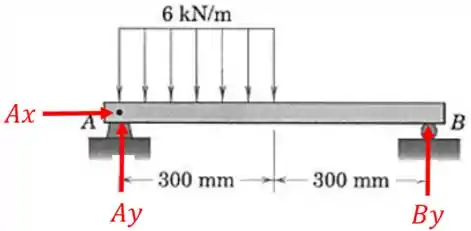
Vamos transformar a carga distribuída em uma única força resultante:
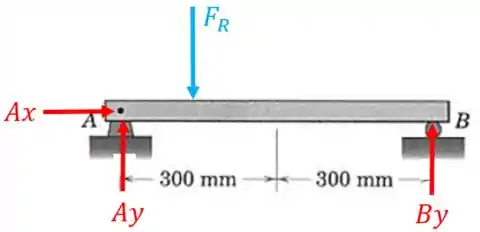
Como a carga distribuída é retangular, a força resultante será:
A localização da força resultante é na metade do comprimento do retângulo:
Então, vamos ter o seguinte diagrama de corpo livre:
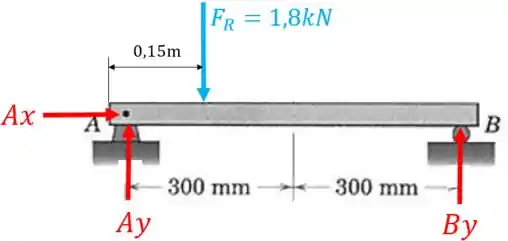
Agora podemos começar o equilíbrio calculando o momento com relação ao ponto , pois neste ponto temos a maior quantidade de forças:
Agora vamos fazer o somatório de forças em cada eixo.
Passo 2
Nosso próximo passo é separar a viga em uma seção à à direita do ponto .
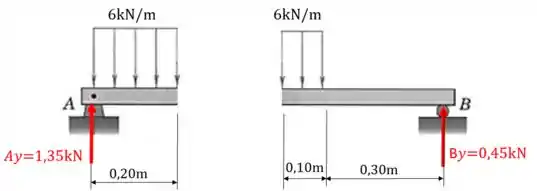
Agora tanto faz a parte da viga que escolhermos para fazer o equilíbrio. Mas vamos ficar com a parte da esquerda.
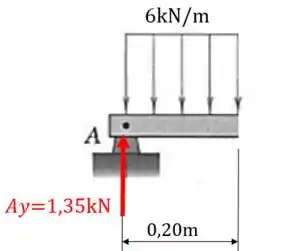
O próximo passo é levarmos tudo que está na parte direita para a seção da parte esquerda. Não esqueça que temos que levar a força e o momento que ela faz na seção! ![]()
Para facilitar, vamos calcular a resultante daquele pedacinho de carga distribuída que tem na parte direita.
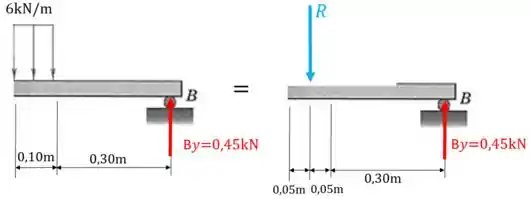
Agora vamos levar as forças e para a seção da parte esquerda com seus respectivos momentos, assim:
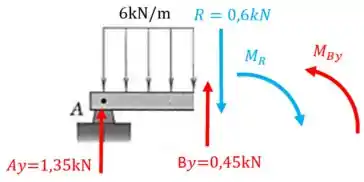
Não esqueça que o sentido da setinha do momento achamos pela regra da mão direita. Vamos calcular esses momentos:
Então, o que temos até agora é:
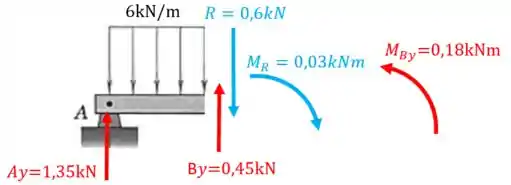
Agora temos que calcular as resultantes das forças e dos momentos nesta seção, assim:
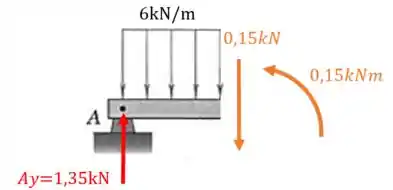
Passo 3
Afinal, qual será o nosso cortante? Será a força resultante naquela seção, ou seja:
Mas ele será positivo ou negativo? É só compararmos com o nosso esqueminha de cortante positivo:
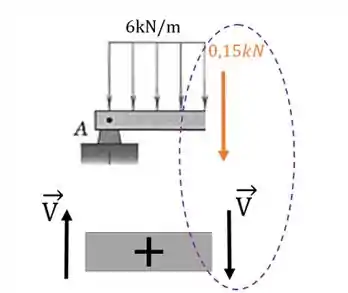
Repare que o nosso cortante aponta para baixo, o mesmo sentido do cortante positivo quando olhamos pela direita, então:
Passo 4
E o momento fletor? Ele será o momento resultante naquela seção, ou seja:
Para sabermos o sinal do momento fletor é só comparar o nosso momento com o esqueminha do momento fletor positivo:
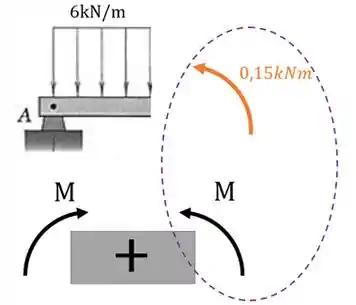
O nosso momento de está apontando para o mesmo sentido do momento positivo, então, o momento fletor nesta seção é: