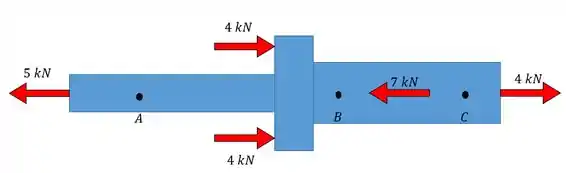
As forças atuam no eixo mostrado, Determina a força normal interna nos pontos e .
Passo 1
E aí, meus queridos e minhas queridas!! Olha só esse problema, perceba que ele já forneceu todas as forças externas atuantes e pede apenas a força normal interna.
Como vamos resolver isso? Bom, se o problema já nos forneceu todas as forças externas então basta fazermos as seções nos pontos dados e calcular a força axial interna:
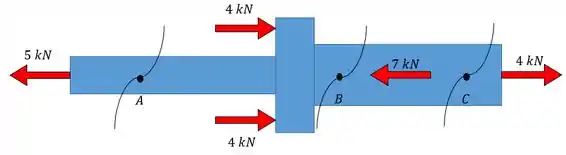
Passo 2
Vamos começar pela seção em :
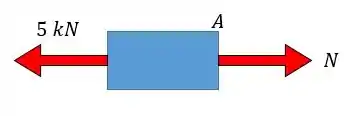
Pessoal, reparem que o problema não pediu nem a cortante nem o momento fletor então não precisamos nos preocupar com esses valores ok!? Só com a normal mesmo, e lembra que a normal é sempre axial ao eixo.
Trazendo a equação da estática para o eixo vamos ter:
Como é positivo então temos uma força de tração, que estica a peça!
Passo 3
Vamos começar pela seção em :
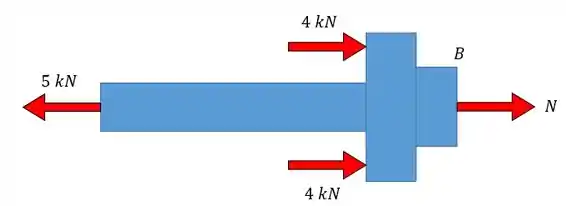
Trazendo a equação da estática para o eixo vamos ter:
Como é negativa então temos uma força de compressão!
Passo 4
Vamos começar pela seção em , dessa vez eu vou fazer o corte pela esquerda (que vai facilitar os cálculos). Reparem que o importante é sempre deixar a força normal para fora da peça!!
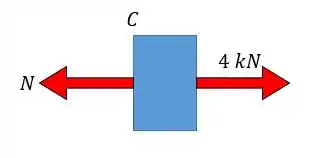
Trazendo a equação da estática para o eixo vamos ter:
Como é positiva então temos uma força de tração!
Se fizéssemos pelo outro lado então daria o mesmo resultado beleza?
Resposta
Para :
Pra :
Para :