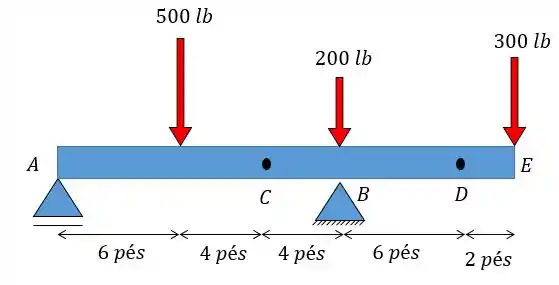
Determine a força de cisalhamento e o momento nos pontos e .

Show de bola! Vamos começar então analisando os apoios e . é um rolete, um apoio de 1° gênero, enquanto é um pino, um apoio de 2° gênero. Dessa forma as reações nesses apoios são dadas como:

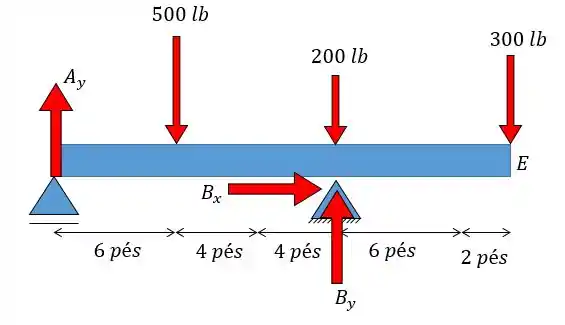
Uhulll!!! Agora é só aplicar as equações da estática:

Para as forças em vamos ter:

Para as forças em :

E finalmente para o momento, aplicado ao ponto e com sentido anti-horário positivo:

Substituindo na equação em vamos ter:

Prontinho! Temos as nossas reações.

Com essas reações vamos fazer um desenho do problema:

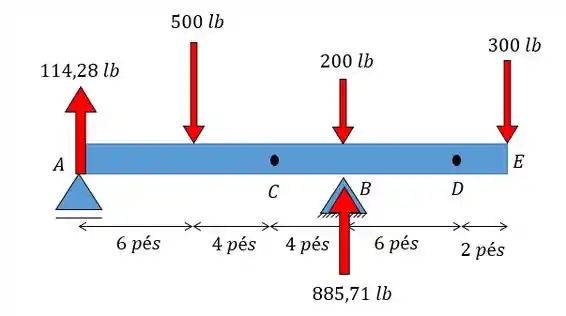
Show! Perceba que eliminamos as incógnitas referentes aos apoios! Agora é só fazermos as seções nos pontos que queremos. Vamos começar pelo ponto :

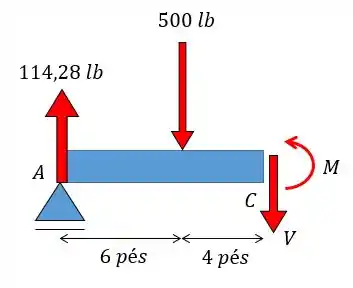
Como não existem esforços horizontais nesse problema eu nem me preocupei em colocar o efeito da normal, já que é nulo, beleza?

Continuando, agora é só fazermos a análise estática.

Para vamos ter:

Agora para o momento, aplicado em e com sentido anti-horário positivo:

Substituindo o valor da força cortante achada anteriormente:

Pronto! Para o ponto já está calculado!

Agora vamos fazer a mesma coisa para o ponto :

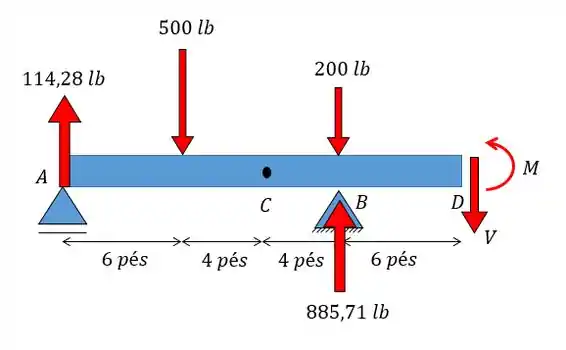
Vamos fazer a análise estática. Para vamos ter:

obs: A gente poderia ter feito pelo outro lado que iria dar menos trabalho! Veja como a cortante é igual à força que “sobrou”. Mas fiz por aqui pra te mostrar como que dá certinho!

Agora para o momento, aplicado em e com sentido anti-horário positivo:

Substituindo o valor da força cortante achada anteriormente:

Novamente poderíamos ter feito pelo outro lado e achado o mesmo valor! Mas é legal fazer pelo menos uma vez assim para ver que é verdade =D