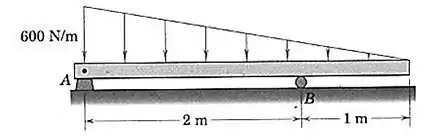
Determine o momento fletor máximo, , para a viga carregada e especifique a distância à direita da extremidade onde ocorre.
Passo 1
O primeiro passo é definir uma equação para a força distribuída. Observe que essa distribuição tem o formato de uma reta inclinada, então podemos escrever:
O valor de pode ser encontrado através pela tangente do triângulo:
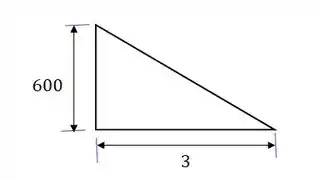
Como a reta está decrescendo, o valor de será negativo!
Assim, a nossa equação do carregamento fica:
E quando temos que , então substituindo isso na nossa equação vamos ter que:
Então, a nossa equação do carregamento distribuído ficou:
Passo 2
Vamos calcular a força resultante da carga distribuída e para isso é só calcularmos a área do triângulo:
E a sua posição em relação ao ponto
Vai ser dada por da altura do triângulo:
Além disso, precisamos calcular as reações em e também. Primeiro vamos fazer o somatório de momentos com relação ao ponto e considerar como positivo o momento no sentido anti-horário:
E agora vamos fazer o somatório de forças verticais:
Passo 3
Sabemos que para achar a equação do cortante precisamos integrar a equação do carregamento e multiplicar o resultado por :
Mas temos que fazer isso para cada intervalo da viga. O primeiro vai de a :
Esse é a constante de integração. Mas qual será o seu valor?
Sabemos que quando , o valor do cortante será igual ao valor da reação:
Então, vamos substituir isso na nossa equação:
Então, a equação do cortante para o trecho da viga que vai de até é:
Portanto, quando , o nosso cortante será:
Passo 4
Agora vamos fazer o mesmo para o outro trecho da viga, ou seja, vamos integrar a equação do carregamento:
Mas repare que a constante de integração mudou para . Mas por que fizemos isso?
Porque no ponto vai ter uma descontinuidade do cortante já que existe a reação neste ponto:
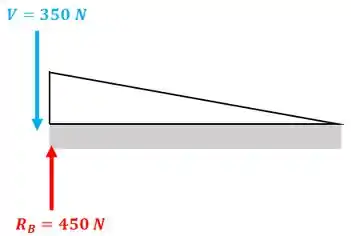
Não esqueça que o cortante é negativo, por isso está apontando para baixo!
Então, nesse novo trecho da viga quando vamos ter que o cortante resultante será:
Vamos substituir isso na nossa equação:
Então, a equação do cortante para o segundo trecho da viga que vai de até é:
Passo 5
Nosso próximo passo é achar a equação para o momento fletor!
Para isso temos que integrar cada equação do cortante que achamos:
Então, para o primeiro trecho da viga vamos ter que:
Sabemos que na extremidade , o momento fletor deve ser zero, então:
Então, a nossa equação fica:
Passo 6
E para o segundo trecho da viga vamos integrar a nossa outra equação do cortante:
Agora sabemos que quando , o momento fletor será zero:
Então, a nossa equação fica:
Passo 7
Para saber onde ocorre o momento máximo é só derivarmos a equação do momento e igualar a zero:
Mas qual das duas equações de momento que achamos?
Repare que na primeira região da viga é que teremos o maior momento, pois tem o maior valor de carregamento, então vamos derivar a primeira equação:
Resolvendo esta equação do segundo grau vamos obter duas raízes:
Como o primeiro resultado é maior que o comprimento da viga, devemos descartá-lo!
Então, o momento máximo ocorre quando
E qual será o seu valor? É só substituirmos esse valor de na nossa equação do momento :