UFABC – Fenômenos Mecânicos – P1 – Questão 6
A força e o ângulo resultante das forças representadas na figura abaixo são:
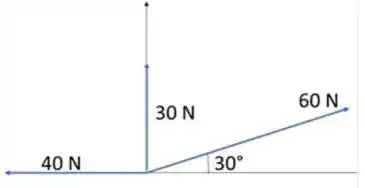
Escolha uma das opções:
- °
- °
Passo 1
Fala galera, tudo bem? Para resolver essa questão precisamos antes de tudo desenhar todas as componentes verticais e horizontais. Saca só a decomposição do vetor de :
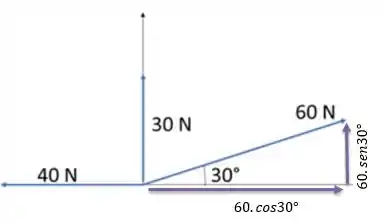
Em roxo estão as componentes. Na vertical temos a componente , e na horizontal temos a componente .
Beleza?
Passo 2
Nosso próximo passo é somar as componentes em uma mesma direção. Assim vamos ter a força resultante na direção e na direção . Começando pela direção .
Vu assumir que todos os vetores que apontem para a direita sejam positivos e que todos os vetores que apontem para a esquerda sejam negativos, ok? Sendo assim temos dois vetores na horizontal: o vetor de que aponta para a esquerda e a componente que aponta para a direita.
A força resultante é a soma dessas duas componentes:
O vetor resultante é positivo, portanto aponta para a direita.
Ok?
Passo 3
Agora a força resultante na direção vertical. Temos outros dois vetores: um vetor de apontando para cima e a componente , também apontando pra cima. Aí a força resultante na direção vertical é:
A resultante vertical aponta para cima pois o sinal é positivo.
Tranquilo?
Passo 4
Aí as componentes do vetor resultante são:
E o vetor força resultante é:
E o módulo de qualquer vetor é a raiz da soma dos quadrados das componentes:
Calma aí, a fórmula é a seguinte:
Agora é só substituir:
E o ângulo dessa força com a horizontal?
Vamos colocar em um plano cartesiano para vermos melhor:
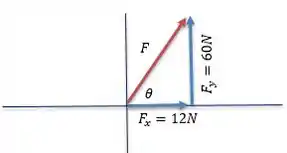
O vetor força resultante está em vermelho, e as componentes estão em azul. O ângulo entre a força e o eixo é , e pode ser calculado através da tangente:
Tranquilo?
Então a força resultante é e o ângulo com a horizontal é , alternativa correta (a).