UFMG – Fundamentos de Mecânica – P1 – Questão Q3
A soma de dois vetores e quaisquer é comutativa, ou seja, . O mesmo acontece com sua subtração, ou seja,
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pediu para verificar se os vetores seguem a propriedade da comutação, ou seja, se a ordem de soma faz diferença no resultado.
Pegando dois vetores quaisquer, vermelho e verde, como na figura abaixo:
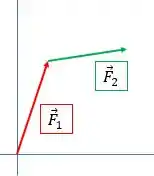
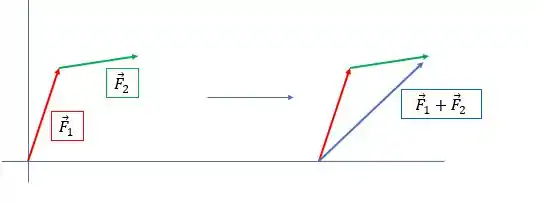
A soma deles vai ser o vetor que une o início do vetor vermelho com a ponta do vetor verde:
Essa afirmação nos disse que uma partícula pode ter uma velocidade vetorial variável, se o módulo da velocidade for constante. Será que isso pode acontecer?
Então, para verificar essa propriedade, precisamos inverter a soma. Desenhar o vetor verde primeiro, depois o vermelho logo na sequência, mantendo tamanho e direção, e achar o vetor soma da mesma maneira: unindo o início do primeiro com a ponta do segundo. E verificar se o resultado é o mesmo
Passo 2
Agora trocando a ordem dos vetores:
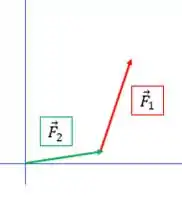
E agora achar o vetor soma:
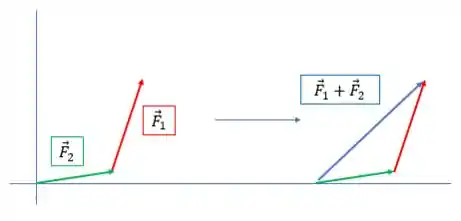
Na soma vetorial encontramos o mesmo valor!
Isso mesmo! A soma de vetores é comutativa!
Vamos ver a subtração?
Passo 3
Agora podemos analisar para a subtração:
Antes de tudo, usando os mesmos dois vetores da situação anterior, precisamos inverter o vetor , pois temos . Fazendo isso, depois é só somar!
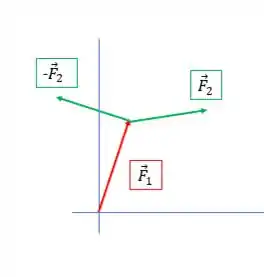
E agora é fazer a soma de :
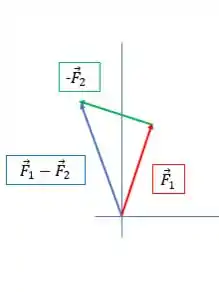
Beleza? Vamos inverter? Agora queremos calcular
Vamos começar invertendo :
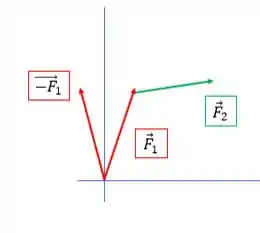
e agora fazer a soma :
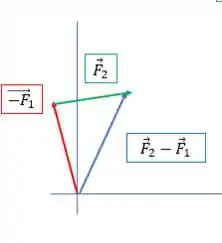
Xi! Não deu o mesmo vetor!
Vamos colocar um vetor do lado do outro para ver melhor:
Mesmo que a soma de vetores seja comutativa, a diferença não é, como podemos verificar.
Beleza?
E é isso!
Espero ter ajudado!