Uma pessoa indo para uma caminhada segue a trajetória mostrada na figura. O passeio
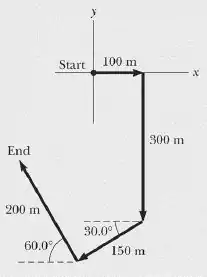
total consiste em quatro trajetórias em linha reta. No final da caminhada, qual é o deslocamento resultante da pessoa medido a partir do ponto de partida (start)?
Passo 1
O problema deu um gráfico que tem uma série de vetores. E nos perguntou qual foi o deslocamento total. Bom, o deslocamento total é aquele em que somamos todos os vetores, mas para isso, precisamos primeiro calcular as componentes de todos eles.

A soma vetorial é diferente da soma algébrica. Para somar vetores, precisamos somar componente a componente. Então para resolver essa questão precisamos redesenhar os vetores, achar suas componentes. Depois disso fazer a soma.
Com isso vamos ter um vetor resultante. Aí podemos aplicar as fórmulas do módulo de um vetor para achar o deslocamento total. Beleza?

Mas relaxa, vou fazer junto com você!
Passo 2
Vamos desenhar os vetores que estão em sequência no deslocamento todos eles partindo da origem do sistema de coordenadas:
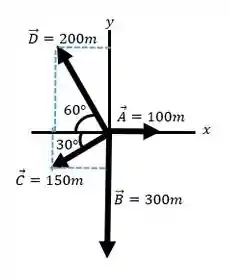
Os vetores e estão sobre os eixos. Para os outros vamos precisar decompor. O vetor A é horizontal, então só tem a componente :
E vetor B é vertical para baixo, então só tem a componente y:
Tranquilo?

O vetor tem componente vertical e horizontal. E as duas são negativas! Então usando seno e cosseno do ângulo de , podemos achar suas componentes:
E o vetor é:
Por fim o vetor aponta para cima na direção vertical, mas para o sentido negativo do eixo x. então sua componente vertical é positiva, mas sua horizontal, negativa. Usando de novo seno e cosseno, podemos achar suas componentes:
Assim, o vetor é:
Beleza?
Passo 3
O vetor resultante vai ser a soma (componente a componente) de todos os vetores:
Fazendo a soma de x com x, e y com y:
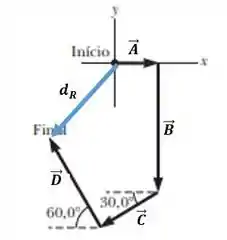 O vetor resultante tem componentes negativas, o que faz sentido com o desenho:
O vetor resultante tem componentes negativas, o que faz sentido com o desenho:
E o deslocamento total é o módulo do vetor resultante:
E é isso!
Espero ter ajudado!