Se e e são não nulos, então:
a) e são paralelos e apontam no mesmo sentido;
b) é perpendicular a ;
c) o ângulo entre e é de .
d) e são paralelos e têm sentidos opostos
e) o ângulo entre e é de .
Passo 1
Lembra da fórmula da soma de dois vetores? Se não se lembra eu te ajudo!
Onde é o ângulo entre os vetores, como visto na figura abaixo:
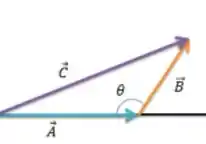
Passo 2
Agora que já lembramos da fórmula, vamos pensar aqui como que faremos pra acontecer isso aqui ó:
Basta lembrarmos do seguinte produto notável:
Substituindo isso na equação anterior, teremos:
Para , temos que . Assim, podemos afirmar que os vetores são paralelos e apontam em sentidos opostos =)
Resposta
d) e são paralelos e têm sentidos opostos
Exercícios de Livros Relacionados
Os vetores deslocamento A → e B → mostrados na Figura P1.34 têm módulos de 3,00m . A direção do vetor A: é θ=30,0 ° . Encontre graficamente a) A → + B → b) A → - B → c) B→ - A → d) A → - 2 B → (Inform
1.92 Quando dois vetores A → e B → são desenhados a partir de um mesmo ponto, o ângulo entre eles é φ . b) Se A → e B → possuem o mesmo módulo, qual deve ser o valor de φ para que o módulo da soma des
Dois operários puxam horizontalmente uma caixa pesada, mas um deles usa o dobro da força do outro. A maior tração está na direção 21,0º de norte para oeste, e o resultante dessas duas forças é 460,0 N
Os vetores unitários i ^ e j ^ apontam para o leste e o norte, respectivamente. Calcule o vetor unitário (em termos de i ^ e j ^ ) das seguintes orientações: (a) Para nordeste, (b) 70 ° medidos no sen
Determine as componentes x e y dos seguintes três vetores do plano x y . (a) Um vetor deslocamento de10m que forma um ângulo de 30 ° no sentido horário a partir do eixo + y . (b) Um vetor velocidade d