Sejam os pontos , , , , e os vértices de um hexeagono regular e seu ponto central. Os vetores e escritos em função dos vetores e são:
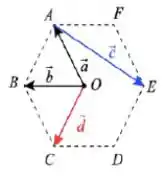
a)
b)
c)
d)
e)
Passo 1
Bom, considerando que o vetor é o único que possui coordenada vertical, podemos ver que tanto pro vetor quanto pro vetor , a resposta deve conter (pois a coordenada vertical de ambos é negativa).
Sendo assim, só tem uma opção que é a letra !
Passo 2
Outra forma é fazer as somas propostas na resposta e ver qual dá certo. Tipo, para a letra a, teríamos:
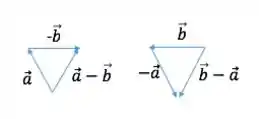
Podemos ver que a primeira soma não corresponde ao vetor , mas a segunda corresponde ao vetor , logo
Passo 3
Se somarmor , e
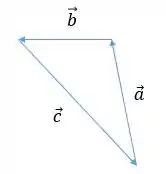
Como vamos e voltamos para o mesmo ponto, temos que a soma desses 3 vetores é nula, assim
Isolando
Resposta
e)