Determine .
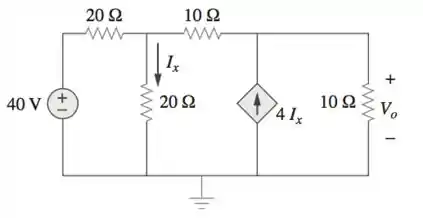
Passo 1
No circuito abaixo, os nós 1 e 2 possuem tensões desconhecias, já que o terceiro está ligado ao terra.
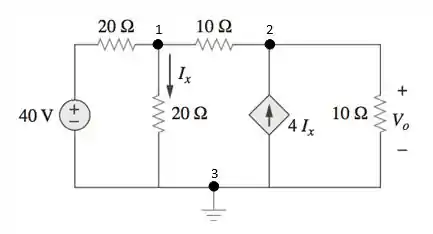
Passo 2
Agora vamos desenhar os sentidos das correntes de cada ramo do circuito e nomear as tensões de cada nó para podermos aplicar a lei das correntes de Kirchhoff.
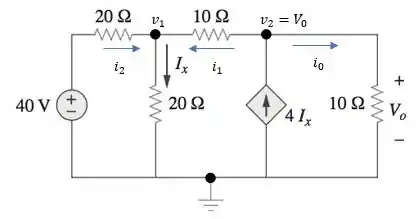
Além disso, a tensão nodal tem própria tensão que se pede no exercício.
Equações de corrente para o nós:
Passo 3
Achar as equações das correntes em relação às tensões nodais:
Passo 4
Substituindo as correntes nas equações de corrente de cada nó:
Simplificando:
Passo 5
Isolando na segunda equação e substituindo na outra, temos:
Pronto!