Escreva as equações nodais usando a abordagem geral para o circuito da figura e resolva:
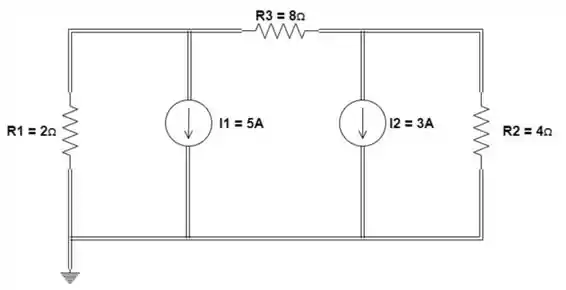
Passo 1
Primeiro, vamos identificar os nós e o terra:
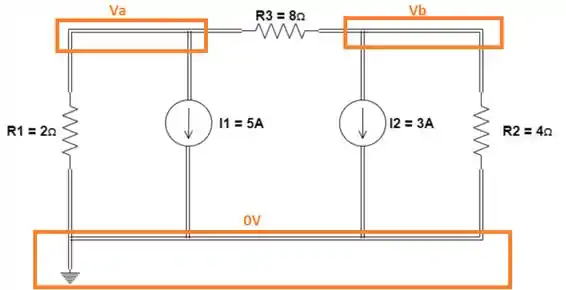
Passo 2
Vamos identificar as correntes que entram e saem dos nós A e B:
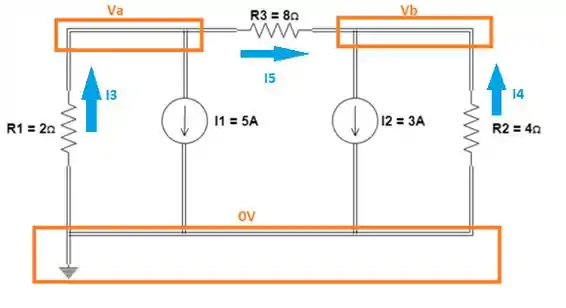
Como vimos que as fontes de corrente estão direcionando as correntes e para entrar no nó de terra, vamos direcionar as correntes e saindo do nó de referência, pois como sabemos a soma das correntes que entram no nó deve ser igual a soma das correntes que saem do nó.
No caso da corrente , escolhemos a corrente no sentido que desejamos.
Passo 3
Através da LKC, as equações para cada nó são:
Nó A:
Pela Lei de Ohm, sabemos que a corrente é igual a tensão em cima do resistor dividido pelo valor da resistência:
No caso da corrente saindo de um nó e entrando em outro, devemos colocar que a tensão é a diferença das tensões do nó de saída da corrente e a tensão do nó de entrada da corrente:
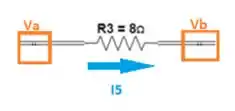
Logo, substituindo na equação :
Nó B:
Passo 4
Encontramos então o sistema:
Subtraindo da primeira equação a segunda equação:
Multiplicando tudo por 4:
Passo 5
Substituindo na primeira equação:
Multiplicando tudo por 8:
Passo 6
Substituindo na seguinte equação:
Ai já encontramos as tensões nodais que era desde o início o nosso objetivo!