Calcule a área determinada pela curva no intervalo .
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo joia?
A gente já aprendeu que “Área determinada pela curva” é simplesmente a integral da curva no intervalo dado. Ou seja, temos que resolver o seguinte:
Lembrando que a integral do é . E fica faltando só substituir os limites de integração.
Aplicando os limites de integração teremos o seguinte:
Sabendo que , ficamos com:
Opa, mas isso não está nas opções. Isso significa que essa forma de resolução está ERRADA.
Pois é, é importante lembrar disso. A integral considera que quando a área está abaixo do eixo , ela é uma “área negativa”. Mas quando a questão pede a área, nós não precisamos seguir essa convenção.
Passo 2
Como corrigir esse problema? Bom, a resposta está nessa imagem da nossa curva, se desenharmos o gráfico da função , teremos:
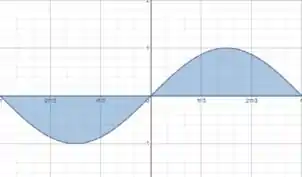
Temos a mesma área dos dois lados, o problema é que a integral “entende” que a área da esquerda é negativa, e isso caba cancelando a integral da direita, levando ao resultado igual a zero, como o que encontramos.
Uma solução pra isso é fazer o seguinte: achar a área em um dos lados e multiplicar por dois!
Ou seja:
E agora que já conhecemos a integral:
Aplicando os novos limites de integração, teremos:
Pronto! Agora sim temos uma resposta coerente, que é a letra A😉
Resposta
- 4