Calcule a área determinada pela curva , entre , .
Passo 1
E aí, tudo joia?
Vamos dar uma olhada no desenho dessa área?
Desenhando o gráfico da função e limitando os valores de e , teremos essa região em pintada em verde:
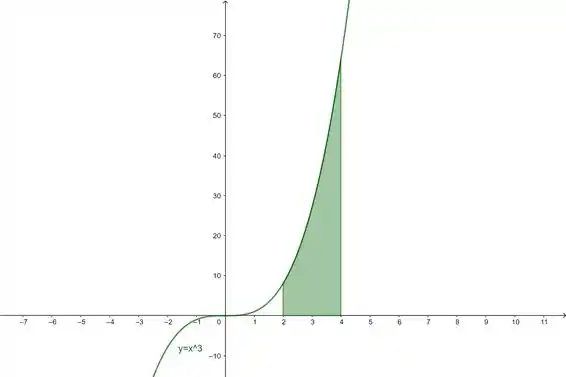
Podemos usar uma integral para calcular essa área:
Que é a integral da curva, no intervalo pedido😉
Passo 2
Vamos resolver essa integral então!
A gente já aprendeu que a integral de uma potência de é isso aqui ó:
Então a nossa é:
Beleza, falta a gente aplicar os limites de integração agora😊
Passo 3
Vamos aplicar os limites, lembrando que a gente faz o resultado do limite maior menos o resultado do limite menor:
Simplificando as frações teremos:
Prontinho! Achamos nossa área, e pra deixar bem bonito a gente acrescenta esse que significa unidade de área! 😊
Resposta
A área determinada pela curva é