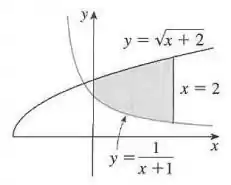
Encontre a área da região sombreada.
Passo 1
Olá, tudo bem?
Precisamos calcular a área da região hachurada (ufa, o enunciado já nos forneceu pelo menos a figura!!!) usando integrais.
É importante lembrar que a área entre as curvas é dada pela integral da função que está em cima menos a função que está em baixo. A função de cima, neste caso, é , enquanto a função de baixo é .
Como a região é limitada à esquerda pelo eixo (reta ) e à direita pela reta , os limites de integração serão e .
Tranquilo até aqui?
Passo 2
Assim, a área pedida será dada por:
Agora vamos achar a integral de cada parte:
Lembrando que , temos que sua integral é
Transformamos o em para podermos somar as frações no expoente e no denominador:
Agora a gente soma em cima e repete em baixo, ficando com:
A fração que está no denominador, nós podemos colocar na frente da função, invertendo ela e deixando ela multiplicando. E o expoente que está fracionário, pode ser escrito em forma de raiz. E ficará assim:
Pronto! Essa foi.
Passo 3
Por outro lado, a integral de é:
Juntando nossas duas soluções, a área é calculada por:
Passo 4
Aplicando os intervalos:
Como , e , segue que
E pronto! Calculamos a área😊