Encontre a área da região sob a curva , no intervalo . Interprete geometricamente o resultado.
Passo 1
Opa! Dá uma olhada no esboço dessa área, pra desenhar a região traçamos o gráfico da função , e desenhamos também o intervalo de entre os pontos e .
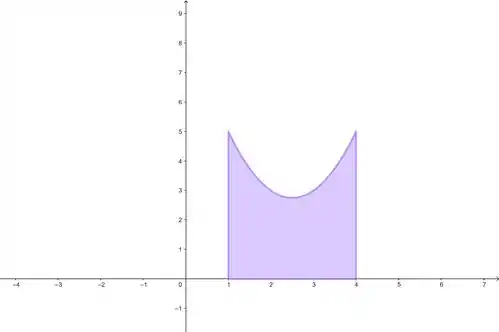
Essa aqui é a intepretação geométrica dela! A voltinha ali é a parábola , e ela está limitada por .
A gente pode calcular essa área fazendo a integral da função no intervalo que foi dado! Ou seja, precisamos calcular isso aqui:
Passo 2
Para resolver essa integral, vamos começar separando essa em outras três, já que nossa função tem três termos:
Lembra que as contantes a gente pode retirar da integral:
E todas essas integrais são de polinômios. Que a gente integral pela regra:
De forma que a integral indefinida é:
Passo 3
Agora a gente tem que substituir os limites de integração:
Lembra que aqui a gente substitui o limite de cima em todos os lugares que tiver na função, e faz a mesma coisa com o limite de baixo, depois subtrai os dois resultados. Assim ó:
Passo 4
Vamos resolver cada potência e arrumar os sinais
A gente pode juntar as frações com denominadores iguais:
Resolvendo as divisões:
Prontinho! Essa é a área da região pedida😉
Resposta
A área da região sob a curva é