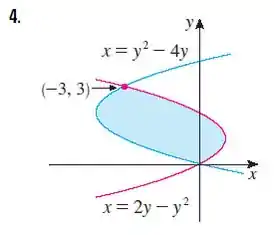
Encontre a área da região sombreada.
Passo 1
Opaaa! Fala ai! Estamos na reta final de cálculo de áreas
Bom galera, antes de começar, vamos dar nomes aos bois!
A gente tem duas funções em relação a
Começando pela rosinha:
Agora para azul:
Já sabemos como se calcula área sobre as curvas, não é?

Passo 2
Beleza, achamos as curvas, mas e os intervalos de integração?
As curvas se cruzam em dois pontos, . Como nossa variável é o y, nós olhamos qual o menor e o maior valor de . Assim, nosso intervalo de integração vai de
Então temos que
Agora ficou fácil, não é?
Passo 3
Como temos as funções e os intervalos, vamos montar a nossa integral, que é desse jeitinho aqui:
Substituindo as funções:
Agora vamos abrir a equação um pouquinho tirando os parênteses e arrumando os sinais:
Ajeitando essa belezinha aí, ficamos apenas com:
Para ficar mais tranquilinho, vamos separar a integral:
Tiramos a constante da integral:
Agora integrando isso daí, temos:
Podemos simplificar na primeira fração, ficando com:
Aplicando os limites de integração:
Agora, ajeitando isso daí, temos:
Sendo assim: