Encontre a área da região sombreada.
Passo 1
Opa! Tudo beleza?
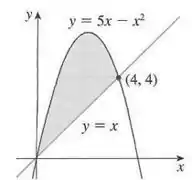
Bom, o exercício pede para acharmos a área da região sombreada! Note que a questão foi legal com a gente e já forneceu o esboço da região.
É importante lembrar que a área entre as curvas é dada pela integral da função que está em cima menos a função que está em baixo.
A função que está em cima é , enquanto a função que está em baixo é . Assim, fazendo a função de cima menos a de baixo, teremos:
Essa será a função que iremos integrar.
Outra coisa que precisaremos é conhecer os limites de integração, e olhando o gráfico podemos perceber que os limites de integração serão e , pois este é intervalo no eixo que delimita a nossa região! Tranquilo? Mãos à obra então!
Passo 2
A área então vai ser dada por:
A gente pode separar essa integral assim:
Ainda podemos retirar a constante pra fora da primeira integral:
E aí a gente vai integrar usando essa regrinha aqui:
Passo 3
Então vai ficar:
Substituindo isso ali em cima, vamos ter:
Podemos simplificar o como , na primeira fração, pra facilitar um pouco as contas:
Show! Vamos aplicar esses limites aí agora😉
Passo 4
A gente aplica os limites fazendo o resultado do limite maior menos o resultado do limite menor. Assim:
Repare que o segundo parênteses vai zera totalmente e só ficaremos com:
Vamos multiplicar o por em cima e embaixo para ficarmos com o mesmo denominador:
Agora a gente pode resolver em cima e repetir o denominador:
E prontinho! Acabamos mais essa😊