Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Áreas

Ver Teoria
Exercício 61234578910

Enunciado

Encontre as áreas da região sombreada.

Passo 1

Fala aí, bora pra mais uma área?

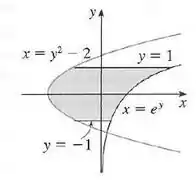
Perceba que nessa aqui temos funções de y , então os intervalos e as variáveis vão ser todas em y , beleza?

É como se as nossas funções estivessem tombadas no eixo x .

Seguinte, a área da região limitada pelas curvas é da seguinte forma:

A = ∫ c d x d i r e i t a - x e s q u e r d a d y

Sendo que como estamos lidando agora com funções de y , a gente analisa qual função tá (na frente” e qual está “atrás”, ao invés de ver qual a que está em cima e qual a que está embaixo.

Concorda que quem tá na frente ali é x = e y e quem tá atrás é x = y 2 - 2 ? Então, x d i r e i t a = e y e x e s q u e r d a = y 2 - 2 .

Passo 2

Beleza, falta a gente achar os limites de integração. Vamos olhar em y . Nossa figura tá indo de y = - 1 a y = 1 , certo? Esses são os nossos limites de integração!

Nossa área, então será calculada por:

A = ∫ - 1 1 e y - ( y 2 - 2 ) d y

Tirando os parênteses e arrumando os sinais, a integral se torna:

A = ∫ - 1 1 e y - y 2 + 2   d y

Podemos separar assim:

= ∫ - 1 1 e y d y - ∫ - 1 1 y 2 d y + ∫ - 1 1 2 d y

Passo 3

Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.

Agora vamos achar as integrais de cada parte das função, usando quatro expressões da Tabela de Integrais Indefinidas:

∫ e x d x = e x + C

∫ c f x d x = c ∫ f x d x

∫ x n d x = x n + 1 n + 1 + C   n ≠ - 1

∫ k d x = k x + C

Passo 4

Aplicando isso nas nossas integrais, temos:

∫ e y   d y = e y + C

∫ y 2   d y =   y 3 3 + C

∫ 2   d y = 2 y + C

Então chegou a hora de colocar os limites de integração (aí nem vai precisar desse C mais)

Passo 5

A = ∫ - 1 1 e y - y 2 + 2   d y

=   e y - y 3 3 + 2 y - 1 1

Agora a gente aplica os limites de integração, lembrando que substituímos o valor do limite superior em todos os lugares que tiver y na função, depois fazemos a mesma coisa com o limites inferior e por fim, subtraímos as duas coisas. Assim ó:

=   e y - y 3 3 + 2 y - 1 1

= e 1 - 1 3 3 + 2 1 - e - 1 - - 1 3 3 + 2 - 1

Agora a gente resolve isso...

Passo 6

Resolvendo as continhas ali...

= e - 1 3 + 2 - 1 e + 1 3 - 2

Podemos tirar os parênteses e concertar os sinais, ficando com:

= e - 1 3 + 2 - 1 e - 1 3 + 2

= e - 1 e - 2 3 + 4

A gente pode multiplicar o 4 por 3 em cima e embaixo pra poder somar com o 2 3 :

= e - 1 e - 2 3 + 4 3 3

= e - 1 e - 2 3 + 12 3

Agora já podemos somar em cima e repetir o denominador do - 2 3   e   6 3 :

A = e - 1 e + 10 3

E pronto! Essa é a nossa área! 😊

Resposta

A = e - 1 e + 10 3