Use a técnica da meia vida para determinar a ordem e a constante de velocidade a partir dos seguintes dados:
![]()
Obs: faça o gráfico de vs e verifique se independe de para ser de 1ª ordem. Se for dependente, faça o gráfico de vs para ver se é de 2ª ordem, etc...
Passo 1
Em um exercício anterior, pra verificar se a reação era de primeira ordem, a gente fez um gráfico de vs t. Porque, para reações de primeira ordem, esse gráfico nos leva a uma reta.
Outra característica das reações de primeira ordem é aquela questão da meia vida. Ou seja, para que a concentração caia pela metade, o tempo transcorrido é sempre o mesmo.
E aqui, vamos traçar o gráfico pedido (de vs ) e verificar a questão da meia vida pra ver se a reação é de primeira ordem.
Caso a meia vida não seja verificada, a gente testa o gráfico de segunda ordem e assim por diante.
Passo 2
Primeiro o gráfico!
Pra cada ponto, devemos calcular e depois aplicar o ln.
O que nos leva aos pontos:
![]()
A partir dos quais, montamos o gráfico:
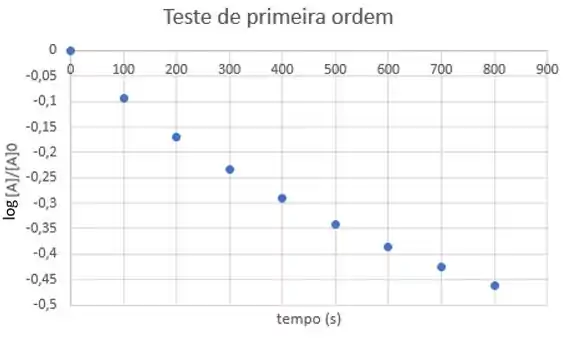
Se a gente tentar traçar uma reta com esses pontos, vai dar ruim!
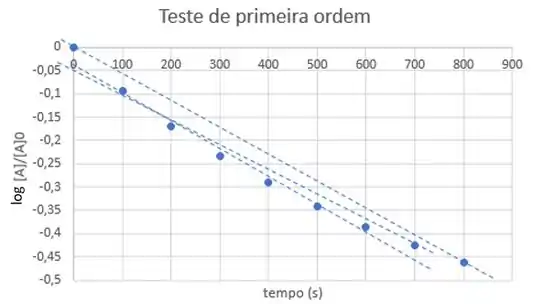
Nenhuma reta se adequa bem aos pontos.
Como, para uma reação de primeira ordem:
O gráfico de vs deveria ser uma reta com coeficiente linear zero e coeficiente angular igual a .
Se não tem reta, não é de primeira ordem!
Passo 3
Quanto à meia vida...
No período de meia vida, a concentração cai pela metade:
Quando o período de meia vida se processa novamente, a concentração cai para um quarto da inicial (metade da metade).
Portanto, o tempo transcorrido para o ln ir de a deveria ser o mesmo tempo transcorrido entre e .
Mas isso não é observado!
Em 400 s temos , mas em 800 s o não está nem perto de .
Como a questão da meia vida não é respeitada, confirmamos que a reação não é de primeira ordem!
Passo 4
Hora de testar a segunda ordem.
A gente deduziu que, para uma reação de segunda ordem:
Com e adotando a notação do exercício:
Ou seja, caso a reação seja de segunda ordem, o gráfico de 1/[A] vs t nos leva a uma reta!
Passo 5
Vamos preparar os pontos:
![]()
E traçar o gráfico!
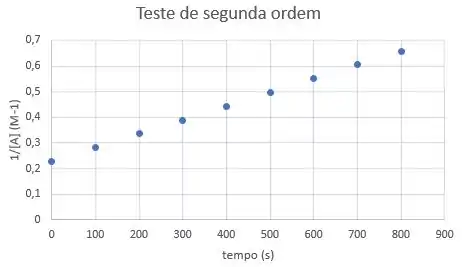
Hmm, agora sim parece uma reta! Conseguimos aproximar os dados por uma única reta!
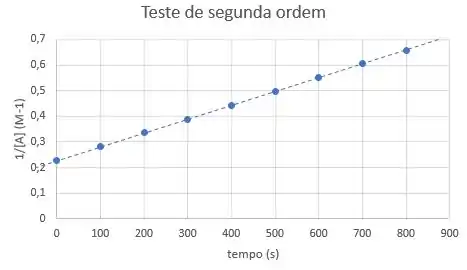
Portanto, a reação se comporta como de segunda ordem em relação ao reagente A.
Resposta
Comportamento de reação de segunda ordem em relação a A.