Uma certa máquina de Carnot absorve de calor de um reservatório a , realiza trabalho e desperdiça calor para um reservatório a . Qual foi o trabalho realizado, a quantidade de calor rejeitada pela máquina e a eficiência?
Passo 1
Falaaa aiiii galeraaaa, animados para começar esta seção?
Espero que siiim ein !!
Bom galerinha, vamos relembrar como funciona uma máquina térmica?
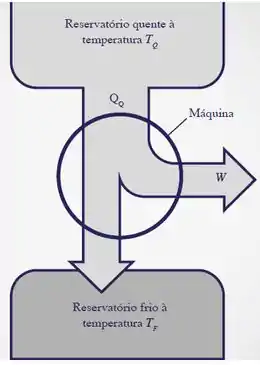
Então, uma máquina térmica é aquele sistema que recebe calor de um reservatório térmico quente (calor resultante da queima de combustíveis, por exemplo) e, posteriormente, devolve um calor para um reservatório térmico frio (como o ambiente ao redor da máquina). A máquina realiza um trabalho útil ao longo do ciclo e por conservação de energia, sabemos que:
A Segunda Lei da Termodinâmica diz que é impossível converter todo esse calor da fonte quente em trabalho, mas existe uma máquina hipotética que foi desenvolvida com o intuito de maximizar a eficiência!!
A máquina que tem a maior eficiência possível é a máquina e Carnot!
Mas em que isso ajuda?
Quando estamos trabalhando com ciclo de Carnot podemos usar a seguinte relação:
Vamos pegar os valores que foram dados no enunciado
E substituir na equação
Vamos multiplicar cruzado
Agora podemos passar o para o outro lado dividindo
Estamos quase lá, vamos multiplicar o numerador
Fazendo essa divisão encontraremos
Shoow de bolaa!! Já achamos uma das variáveis!!
Passo 2
Como temos a quantidade de calor enviado para a fonte fria, e a quantidade de calor absorvido da fonte quente, Podemos usar a relação que já vimos no Passo para achar o trabalho:
Isolando o , o termo passa para o outro lado com o sinal oposto:
Substituindo:
Mais uma variável achada com sucesso !!
E agora?!
Vamos achar a eficiência !!
Que tal usar a fórmula que já conhecemos para as Máquinas Térmicas?
Substituindo:
Para transformar em porcentagem nós multiplicamos por :
E assim nós finalizamos esta questão !!