Na região Atártica monta-se um laboratório. A temperatura é no exterior e deve ser mantida a no interior. Nessas condições, o laboratório perde calor para o ambiente com um apotência de Esse calor deve ser reposto por uma termo bomba acionada por um motor Diesel. Qual deve ser o menor consumo teórico de energia pela termo bomba?
Passo 1
Animados para mais uma?!
Bom, vamos começar entendendo o que está acontecendo.
Precisamos que dentro do laboratório fique com uma temperatura maior que o meio externo. Então o que precisamos é de um aquecedor.
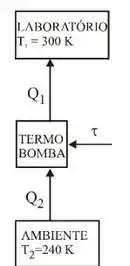
Agora olhando para o esquema da questão. Para que o calor flua da fonte fria (ambiente) para a fonte quente (laboratório), precisamos fornecer trabalho à termo bomba.
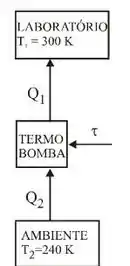
Por isso temos a seta do calor da fonte fria e o trabalho para dentro da máquina e o calor da fonte quente para fora dela.
Então, pela conservação da energia
Maravilha! Já entendemos o que está acontecendo, guardem isso no coração 😊
Passo 2
Agora vamos ver as informações do enunciado
Essa última informação da potência significa que a cada segundo, a máquina perde de calor, já que a unidade de Watts pode ser escrita como
Então vamos combinar uma coisa: Trataremos tudo com relação a segundo. No final entenderemos o que vai acontecer para outros valores de tempo, belezinha?
Com isso, teremos
E tem uma informação importante que não pode passar despercebida. Ele pergunta “Qual deve ser o menor consumo teórico de energia pela termo bomba?”, então precisamos da máquina mais eficiente possível, não é mesmo?
E qual é a máquina mais eficiente que podemos construir? Isso aí, a máquina de Carnot!!
Então podemos escrever a seguinte relação:
Agora vamos substituir os valores que que anotamos
Para encontrar o podemos multiplicar cruzado
Agora passaremos o para o outro lado dividindo
Estamos quase lá! Para resolver essa conta, vamos fazer a multiplicação do com o e dividir por (depois só repetimos a potência de )
Passo 3
Mas não é bem isso que precisamos, certo?
O que queremos é o “menor consumo teórico de energia”. Isso quer dizer que precisamos descobrir o trabalho mínimo que precisamos fornecer à máquina para ela realizar essa tarefa
E para isso vamos usar a conservação da energia que vicmo lá no Passo
Isolando o , o termo passa para o outro lado com o sinal oposto:
Como já sabemos que
Podemos substituir na equação
Lembrando que:
Podemeos transformar o trabalho em:
Esse é o valor do trabalho que deve ser fornecido à termo bomba a cada segundo (lembra que consideramos o tempo como segundo?)
E assim achamos mais uma !!