Dois motores térmicos de Carnot são acoplados, operando o par entre as temperaturas e Qual o rendimento total desse sistema?
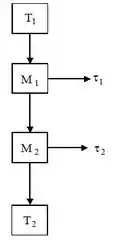
Passo 1
Vamos começar entendendo esse desenho?
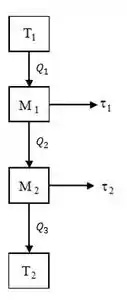
![]()
O rendimento total dessa máquina, assumindo que ela opera como máquina de Carnot leva em consideração apenas as temperaturas da fonte fria e da fonte quente, certo?
Vamos relembrar da fórmula?
O enunciado diz que temos duas máquinas acopladas e que cada uma opera em um ciclo de Carnot. Podemos olhar esse sistema inteiro como sendo um único sistema operando com o ciclo de Carnot entre as temperaturas
Então:
Fazendo primeiro a divisão entre e , encontramos
E essa subtração nos dá, aproximadamente
Para obter em porcentagem, multiplicamos por :
Essa foi molezinha, não foi?