Uma máquina térmica ideal opera em ciclos de Carnot entre as temperaturas e Operando como refrigerador, a máquina retira da fonte fria em cada ciclo Determine o calor cedido à fonte quente, o trabalho consumido e o coeficiente de desempenho.
Passo 1
Agora nós vamos entrar num ponto bem legal, os refrigeradores!!
Bom galerinha, vamos relembrar como funciona?
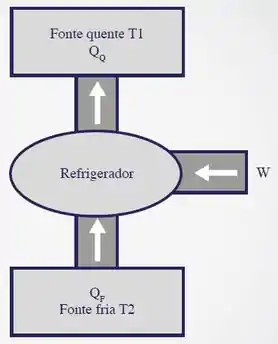
Então, os refrigeradores são máquinas térmicas operando no sentido inverso. Portanto, o refrigerador utiliza o trabalho fornecido de outro lugar (pode ser por eletricidade, por exemplo) para retirar calor de uma fonte fria e levar para uma fonte quente!!
Então, a conservação de energia nos diz que:
Beleza !! Vamos guardar esta informação no coração, ok?
Aqui também vale aquela relação que já vimos paa ciclos de Carnot
Como a quantidade de calor cedido pela máquina, , é o que queremos saber, vamos passar para o outro lado multiplicando:
O problema disse que:
Substituindo:
Passo 2
Agora, precisamos achar o trabalho, certo?
E para isso vamos usar a conservação da energia que vimos lá no Passo
Isolando o , o termo passa para o outro lado com o sinal oposto:
O problema nos disse que:
Substituindo:
E assim achamos mais uma!!
Passo 3
E para finalizar precisamos achar o coeficiente de desempenho, vamos rever a fórmula?
Substituindo:
E assim nós finalizamos esta questão!!