O gás perfeito contido em uma máquina térmica retira de calor da fonte quente e rejeita para a fonte fria em cada ciclo. A temperatura da fonte fria é e a da fonte quente é . Determine para cada ciclo:
- o trabalho realizado;
- o rendimento da máquina;
- o rendimento máximo teórico da máquina
Passo 1
Vamos lá pessoa, agora para fechar com chave de ouro!!
Vamos começar analizando as informações que foram dadas no enunciado
Cuidado com os índices! Tudo o que tiver índice é referente a fonte quente e índice tudo o que tiver índice é referente a fonte fria.
Olhando para esses dados podemos ver que as temperaturas não estão no Sistema Internacional de unidades, temos que passar para Kelvin!
Lembram da formulinha para passar de para ? Não?? Vou refrescar sua memória
Agora é só substituir os valores das temperaturas e fazer a conversão
Show! Agora nossas unidades estão legais 😊
Passo 2
Na letra a) é pedido o trabalho realizado pela máquina a cada ciclo. Vamos fazer o esqueminha da máquina térmica
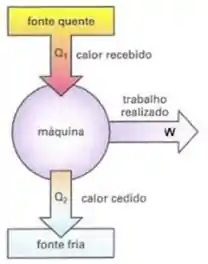
A máquina recebe calor da fonte quente, transforma esse calor em trabalho e cede calor para a fonte fria . Então podemos dizer que, pela conservação da energia
Maravilha! Já temos e
Agora é só substituir
Passando o para o outro lado com sinal contrário, temos
E finalmente
Passo 3
Beleza, agora vamos para a letra b). Ele nos pede o rendimento dessa máquina.
E como calculamos o rendimento mesmo? Assim ó
Como acabamos de descobrir o e já temos o
Podemos cortar esses zeros todos para simplificar a conta
E fazendo essa divisão encontramos
Se quisermos transformar isso em porcentagem, basta multiplicar por
Passo 4
Para finalizar, vamos fazer a letra c). Ela é bem parecida com a letra b), mas tem um detalhe importante na frase “o rendimento máximo teórico da máquina”.
Então o enunciado quer que a gente diga qual é o rendimento da máquina mais eficiente possível. Essa máquina tem um nome, é a máquina de Carnot!!
E para isso temos uma formulinha especial para calcular o rendimento da máquina de Carnot
Como já sabemos que
Substituindo na equação do rendimento
Podemos cortar os zeros para simplificar a divisão
Fazendo a divisão do pelo
E finalmente teremos
Para deixarmos a resposta em forma de porcentagem é só multiplicar por
Uhuuuulll! Encerramos a questão 😊