Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RLC sem fonte

Ver Teoria
Exercício 41235678910

Enunciado

A chave do circuito abaixo muda da posição A para B em t = 0 (observe atentamente que a chave tem de se conectar ao ponto B antes de ela desfazer a conexão em A , um interruptor). Determine i ( t ) para t > 0 .

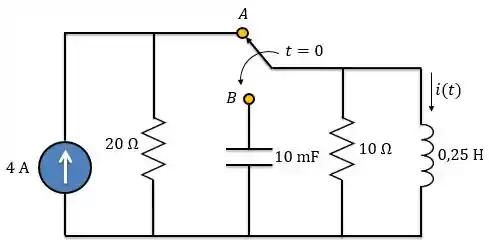
Passo 1

Vamos considerar que a chave estava na posição A por um longo tempo antes de t = 0 . Logo, o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto-circuito.

Passo 2

Logo, para instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

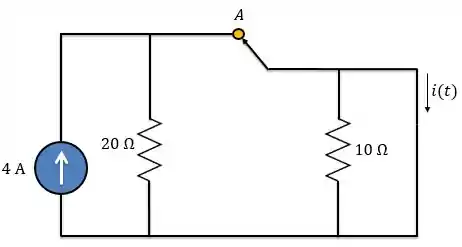
Como a corrente sempre escolhe o caminho mais fácil para ela circular, toda a corrente fornecida pela fonte de corrente passará pelo curto-circuito (indutor).

i 0 - = 4   A

Além disso, o capacitor está desconectado do circuito, logo não tem tensão em seus terminais.

v 0 - = 0

Passo 3

Agora, vamos analisar o circuito quando a chave muda para posição B . Em t = 0 + , podemos considerar o seguinte circuito:

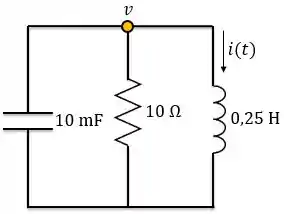
Esse circuito nós conhecemos bem. É o R L C paralelo sem fonte. Encontraremos a expressão da tensão nesse circuito utilizando α e ω 0 . Sabemos que para esse circuito

α = 1 2 R C               e             ω 0 = 1 L C

Passo 4

Substituindo os valores dos elementos do circuito, temos:

α = 1 2 10 0,01

α = 5

e

ω 0 = 1 0,25 0,01

ω 0 = 20

Passo 5

Como α < ω 0 , temos o caso de resposta subamortecida e vimos na teoria que sua solução é:

v t = e - α t ( A cos ⁡ ω d t + B sin ⁡ ω d t )

Sendo

ω d = ω 0 2 - α 2

ω d = ( 20 2 - 5 2 = 19,365

Substituindo esses valores, temos:

v t = e - 5 t ( A cos ⁡ 19,365 t + B sin ⁡ 19,365 t )

Passo 6

Encontramos uma expressão para a tensão do circuito, mas o que queremos determinar é a corrente no indutor i t para t > 0 . Sabemos que no indutor:

i t = 1 L ∫ 0 t v   d t

Logo,

i t = 1 0,25 ∫ 0 t e - 5 t ' ( A cos ⁡ 19,365 t ' + B sin ⁡ 19,365 t ' )   d t '

Mas não precisamos fazer essa integral, ainda bem né? Vou te explicar o porquê.

Como a nossa expressão para v ( t ) é formada por exponenciais, senos e cossenos, só as constantes sofrerão alterações e se tornarão em novas constantes. Logo, podemos dizer que a corrente i ( t ) será:

i t = e - 5 t ( D cos ⁡ 19,365 t + F sin ⁡ 19,365 t )

Onde D e F , são as novas constantes.

Passo 7

Agora, precisamos encontrar os valores das constantes D e F . Como se trata de uma EDO de segunda ordem, precisamos da condição inicial da corrente i ( 0 + ) e de sua primeira derivada d i ( 0 + ) / d t .

Nós calculamos i 0 - = 4 . Como no indutor a corrente não varia instantaneamente:

i 0 + = 4

Portanto,

i 0 + = e - 5 0 D cos ⁡ 19,365 0 + F sin ⁡ 19,365 0

Como, s i n ⁡ ( 0 ) = 0 e cos ⁡ 0 = 1 , temos:

i 0 + = D = 4

D = 4

Como o circuito é paralelo, a tensão v é a mesma para todo o circuito e como no capacitor a tensão não pode variar instantaneamente

v 0 - = v 0 + = 0

Logo, no indutor temos:

v 0 + = 0,25 d i 0 + d t

0 = 0,25 d i 0 + d t

d i 0 + d t = 0   A / s

Passo 8

Derivando i t ,   temos

d i t d t = d d t [ e - 5 t D cos ⁡ 19,365 t + F sin ⁡ 19,365 t )

Então, pela regra do produto:

d i t d t = - 5 e - 5 t ( D cos ⁡ 19,365 t + F sin ⁡ 19,365 t ) + e - 5 t ( - 19,365 D sin ⁡ 19,365 t + 19,365 F cos ⁡ 19,365 t )

Logo,

d i 0 + d t = - 5 D + 19,365 F = 0

Como D = 4 ,

- 5 ( 4 ) + 19,365 F = 0

F = 20 19,365

F = 1,033

Passo 9

Portanto, substituindo os valores das constantes, nossa solução final será

i t = e - 5 t ( 4 cos ⁡ 19,365 t + ( 1,033 ) sin ⁡ 19,365 t )

i t = e - 5 t ( 4 cos ⁡ 19,365 t + 1,033 sin ⁡ 19,365 t )   A

Resposta

i t = e - 5 t ( 4 cos ⁡ 19,365 t + 1,033 sin ⁡ 19,365 t )   A

Exercícios de Livros Relacionados

Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
A equação que descreve a tensão em um circuito RLC é d 2 v d t 2 + 5 d v d t + 4 v = 0 Se v(0) = 0, dv(0)/dt = 10 V/s, obtenha v(t).
Sabe-se que a corrente no circuito da Figura P6.35 é io = 2e-5.000t(cos 1.000t + 5 sen 1.000t) Apara t $ 0+. Determine v1(0+) e v2(0+).
Para o circuito da Figura 8.58, a corrente inicial no indutor (em t = 0) é:(a) 0 A (b) 2 A (c) 6 A (d) 12 A
Obtenha v ( t ) para t0 no circuito da Figura 8.73.