Um circuito em série possui Que tipo de amortecimento é apresentado pelo circuito?
Passo 1
De acordo com o enunciado, temos o seguinte circuito:
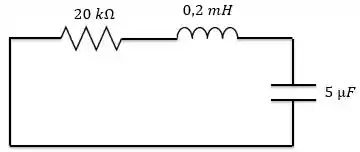
Passo 2
Agora vamos encontrar o fator de amortecimento e a frequência natural não-amortecida .
e
Como a resposta é superamortecida.
Resposta
Superamortecido
Exercícios de Livros Relacionados
Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
A equação que descreve a tensão em um circuito RLC é d 2 v d t 2 + 5 d v d t + 4 v = 0 Se v(0) = 0, dv(0)/dt = 10 V/s, obtenha v(t).
Sabe-se que a corrente no circuito da Figura P6.35 é io = 2e-5.000t(cos 1.000t + 5 sen 1.000t) Apara t $ 0+. Determine v1(0+) e v2(0+).
Para o circuito da Figura 8.58, a corrente inicial no indutor (em t = 0) é:(a) 0 A (b) 2 A (c) 6 A (d) 12 A
Obtenha v ( t ) para t0 no circuito da Figura 8.73.