A corrente em um circuito é descrita por
Se e determine para
Passo 1
Como o enunciado falou da corrente em um circuito , significa que a mesma corrente passa por todos os elementos. Portanto, o circuito é um série.
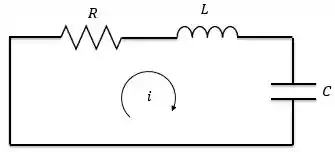
Passo 2
O enunciado disse que a corrente é descrita assim
Vamos encontrar a solução de EDO de segunda ordem. Ela possui a seguinte equação característica:
Logo,
Então,
Passo 3
Temos duas raízes reais e iguais, . Logo, para esse caso a solução da EDO é
Substituindo o valor de
Passo 4
Agora, precisamos encontrar os valores das constantes e . Para isso, vamos utilizar as nossas condições iniciais
Da primeira condição,
Passo 5
Calculando a derivada de , temos:
Usando a nossa segunda condição inicial,
Passo 6
Portanto, substituindo os valores das constantes, nossa solução final será